Pilnie prosze o pomoc!!!

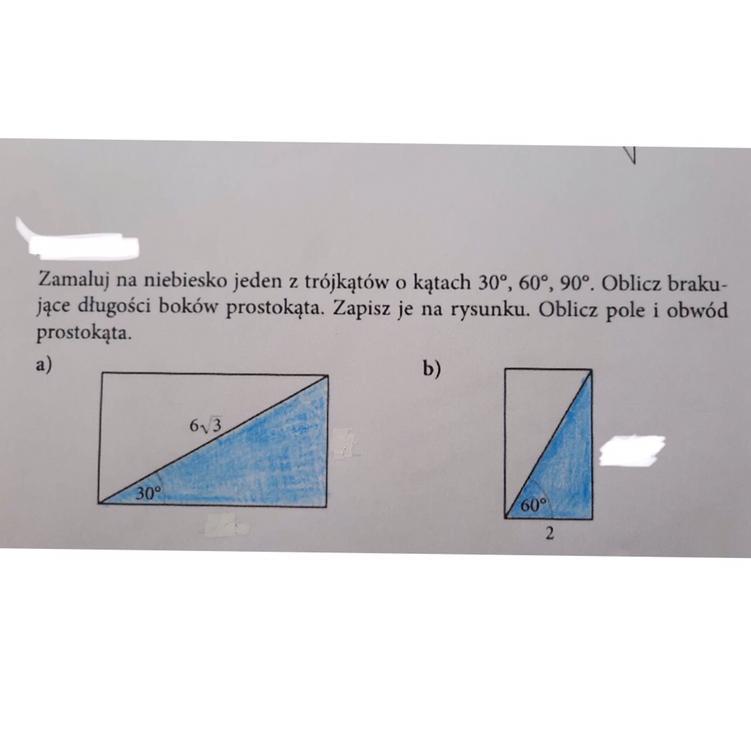
W zadaniu poprawnie zamalowano na niebiesko trójkąty prostokątne o kątach 30°, 60°, 90°.

Rozwiązania:

a)

P = 27√3

Obw = 6√3 + 18

b)

P = 4√3

Obw = 4√3 +4

Obliczenia poniżej.

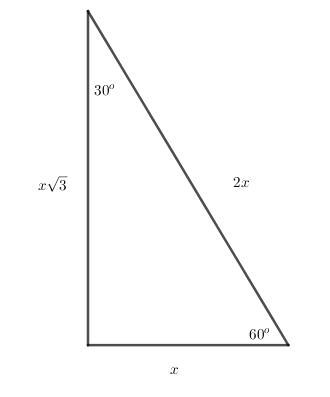
Chcąc obliczyć długości boków tych prostokątów skorzystamy z tychże własności trójkąta o podanych wyżej kątach. Rysunek pomocniczy w załączniku.

Przypomnijmy wzory:

- pole prostokąta:

[tex]P = a\cdot b[/tex]

- obwód prostokąta:

[tex]Obw = 2a + 2b[/tex]

gdzie:

a, b - boki prostokąta

a)

Z własności trójkąta o podanych kątach:

[tex]2x = 6\sqrt{3} | : 2 \\\\x =a = 3\sqrt{3} \\\\[/tex]

[tex]b = x\sqrt{3} = 3\sqrt{3} \cdot \sqrt{3} = 3 \cdot \sqrt{9} = 3 \cdot 3 = 9[/tex]

Obliczamy pole:

[tex]\boxed{P = a \cdot b = 3\sqrt{3} \cdot 9 = 27\sqrt{3}} \\\\[/tex]

Obliczamy obwód:

[tex]\boxed{Obw = 2a + 2b = 2 \cdot 3\sqrt{3} + 2 \cdot 9 = 6\sqrt{3} + 18} \\\\[/tex]

b)

Z własności trójkąta o podanych kątach:

[tex]x = a = 2\\\\b = x\sqrt{3} = 2\sqrt{3}[/tex]

Obliczamy pole:

[tex]\boxed{P = a \cdot b = 2 \cdot 2\sqrt{3} = 4\sqrt{3}} \\\\[/tex]

Obliczamy obwód:

[tex]\boxed{Obw = 2a + 2b = 2 \cdot 2 + 2 \cdot 2\sqrt{3} = 4\sqrt{3} + 4}[/tex]

#SPJ2

a) W wyniku podbojów napoleońskich państwem zależnym od Francji stało się Królestwo Neapolu.

b) Bitwa pod Austerlitz 1805 rok (pomarańczowe pole "Cesarstwo Austriackie" - zaznacz tam miejscowość Austerlitz)

c) W wyznaczonym miejscu wpisz Cesarstwo Francuskie

w b) podkreśl Austerlitz

Odpowiedź:

1. określenie wydarzenia z 1934 roku podczas którego zamordowano przywódców SA w Niemczech.

Noc Długich Noży

2. obozy pracy w Rosji Sowieckiej a następnie ZSRR

Gułag

3. Spółdzielcze gospodarstwo rolne w ZSRR

Sowchoz

4. tym pojęciem określano bogatych chłopów w ZSRR

Kułak

5 skrót nazwany partii nazistowskiej w Niemczech

NSDAP

6 tytuł jakim określano przywódcę faszystowskich Włoch

Duce (Ducze po polsku)

Wyjaśnienie: