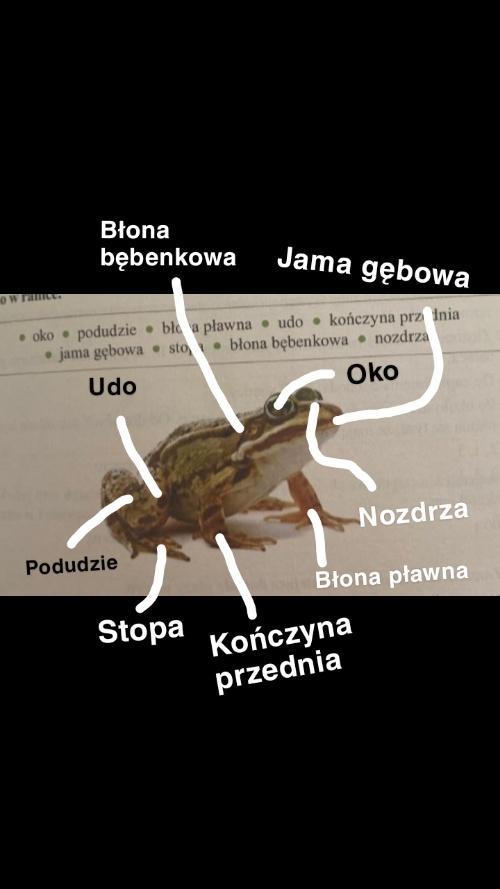
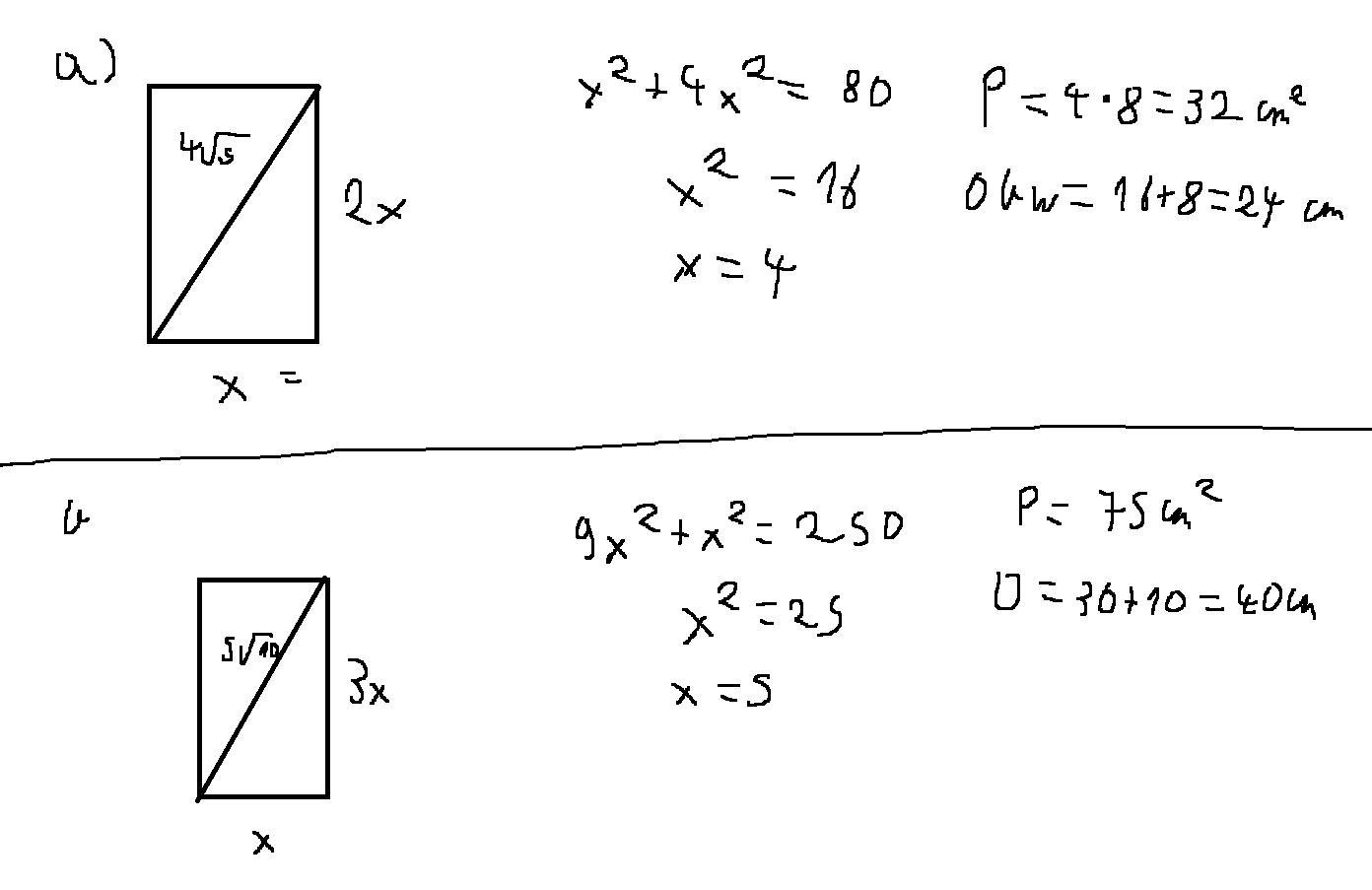4. Zaznacz i podpisz na ilustracji elementy budowy Zaby, których nazwy zamiesz- B czono w ramce. • oko podudzie błona pławna • udo • kończyna przednia • jama gębowa • stopa • blona bębenkowa nozdrza nazwy

Odpowiedź:

1. nieprawda, musisz się uspokoić, wierzę, że tym razem Ci się uda!

2. To może spróbuj porozmawiać z innymi dziećmi. napewno cię polubią i to sprawi, że już nie będziesz sam!

3. czasami tak bywa, ale głowa do góry nie można się załamywać, spróbuj ten czas jakoś kreatywnie wykorzystać.

7.

a) 90x km

b) 6km - 6 000m

6 000t m

c) 1h-60 min

60 m n km

8.

a) (n+100):4

b) 3(m+n)

c) ¾(m-n)

d) ½(m+n-6)

9.

(n-3):12

Odpowiedź:

7.

a) 90x km

b) 6000t m

c) 60nm km

8.

a) 1/4(n+100)

b) 3(m+n)

c) 3/4(m-n)

d) 1/2(m+n-6)

9.

n-3/12kg

/ - kreska ułamkowa

Szczegółowe wyjaśnienie:

Mam nadzieję że pomogłam

wszystko jest sprawdzone bo wczoraj na lekcji online to robiliśmy

She wants make a spaghetti so she need:

pasta

tomato sauce

parmesan

Mam nadzieję ze wszystko czytelnie, w razie pomocy pisz w komentarzu.

Odpowiedź i wyjaśnienie:

a)

a = pierwszy bok

2a = drugi bok

4√5 cm = przekątna

Długości boków tego prostokąta obliczam korzystając z twierdzenia Pitagorasa:

a² + (2a)² = (4√5)²

a² + 4a² = 16 * 5

5a² = 80. /:5

a² = 16

a = 4

a = 4 cm

2a = 2 * 4 cm = 8 cm

Boki tego prostokąta mają długości:

4 cm i 8 cm

P = a * b

P = 4 cm * 8 cm = 32 cm²

Obw = 2 * a + 2 * b

Obw = 2 * 4 cm + 2 * 8 cm = 8 cm + 16 cm = 24 cm

Odp: pole tego prostokąta wynosi 32 cm², a obwód wynosi 24 cm.

b)

a = pierwszy bok

3a = drugi bok

5√10 cm = przekątna

a² + (3a²) = (5√10)²

a² + 9a² = 25 * 10

10a² = 250. /:10

a² = 25

a = 5

a = 5 cm

3a = 3 *5 cm = 15 cm

Boki tego prostokąta mają długości:

5 cm i 15 cm

P = a * b

P = 5 cm * 15cm = 75 cm²

Obw = 2 * a + 2 * b

Obw = 2 * 5 cm + 2 * 15 cm = 10 cm + 30 cm = 40 cm

Odp: pole tego prostokąta wynosi 75 cm², a obwód wynosi 40 cm.