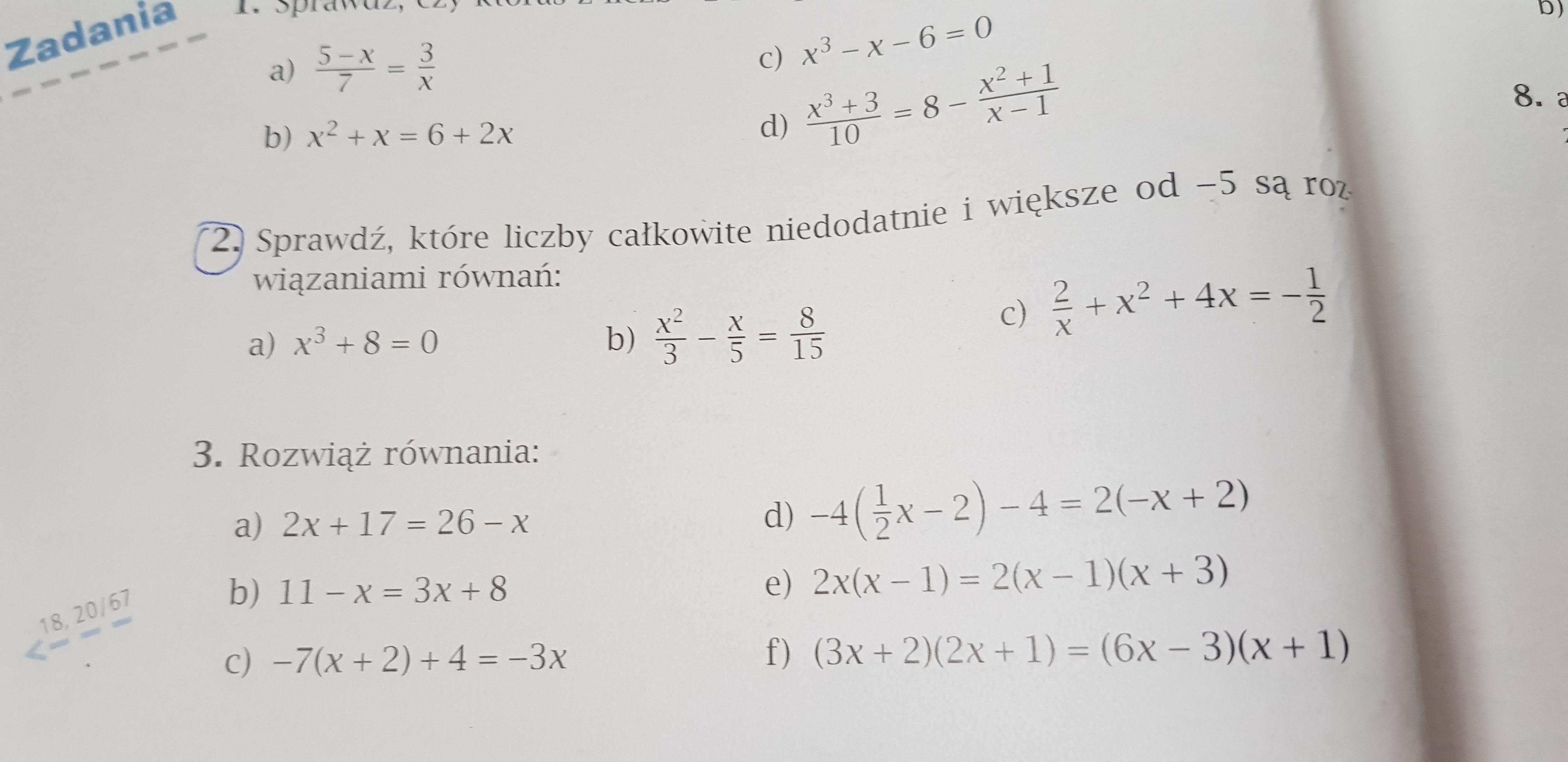ustal, jakie cząstki należy wpisać w miejsca znaków zapytania, aby otrzymać równania reakcji jądrowych. PLISSSSSSS POTRZEBNE BARDZO DAM NAJ​

Odpowiedź:

Wyjaśnienie:

1/  Die Wohnung besteht aus zwei Zimmern und einer Küche. (1 B)

2/ Der Vater arbeitet im Arbeitszimmer. ( 2 A)

3/ Wir zeigen den Garten. (3 B)

Odpowiedź:

1/  Die Wohnung besteht aus zwei Zimmern und einer Küche. (1 B)

2/ Der Vater arbeitet im Arbeitszimmer. ( 2 A)

3/ Wir zeigen den Garten. (3 B)

Wyjaśnienie: mam nadzieję że pomogłam (:  

<3

Odpowiedź:

zad 2

Liczby niedodatnie całkowite większe od - 5 to liczby:

- 4 , - 3 , - 2 , - 1

x² + 8 = 0

(- 4)² + 8 = 0

16 + 8 = 24 ≠ 0

L ≠ P

(- 3)² + 8 = 0

9 + 8 = 17 ≠ 0

L ≠ P

(- 2)² + 8 = 0

4 + 8 = 12 ≠ 0

L ≠ P

(- 1)² + 8 = 0

1 + 8 = 9 ≠ 0

L ≠ P

Żadna liczba z podanych nie spełnia równania  

Poza tym każda liczba ze zbioru liczb rzeczywistych podniesiona do kwadratu jest ≥ 0 więc nie ma takiego x w całym zbiorze liczb rzeczywistych spełniających to równanie

x ∈ ∅ (zbiór pusty)

b)

x²/3 - x/5 = 8/15 | * 15

5x² - 3x = 8

5 * (- 4)² - 3 * (- 4) = 5 * 16 + 12 = 8

80 + 12 = 8

92 ≠ 8

L ≠ P

5 * (- 3)² - 3 * (- 3) = 8

5 * 9 + 9 = 8

45 + 9 = 8

54 ≠ 8

L ≠ P

5 * (- 2)² - 3 * (- 2) = 8

5 * 4 + 6 = 8

20 + 6 = 8

26 ≠ 8

L ≠ P

5 * (- 1)² - 3 * (- 1) = 8

5 * 1 + 3 = 8

5 + 3 = 8

8 = 8

L = P

Liczba (- 1) spełnia warunki równania

c)

2/x + x² + 4x = - 1/2

założenie:

x ≠ 0

2/(- 4) + (- 4)² + 4 * (- 4) = - 1/2

- 1/2 + 16 - 16 = - 1/2

- 1/2 = - 1/2

L = P

Liczba (- 4) spełnia równanie

2/(- 3) + (- 3)² + 4 * (- 3) = - 1/2

- 2/3 + 9 - 12 = - 1/2

- 2/3 - 3 = - 1/2

- 3 2/3 ≠ - 1/2

2/(- 2) + (- 2)² + 4 * (- 2) = - 1/2

- 1 + 4 - 8 = - 1/2

- 5 ≠ - 1/2

2/(- 1) + (- 1)² + 4 * (- 1) = - 1/2

- 2 + 1 - 4 = - 1/2

- 5 ≠ - 1/2

L ≠ P

Tylko (- 4) spełnia warunki równania

Odpowiedź:

Przeciwnikiem byli Persowie