Pomocy! oznaczam najlepszą odpowiedz

Odpowiedź:

Szczegółowe wyjaśnienie:

a) -3x*1/3x=-3/1x*1/3x=-3/3x=-1x

b) -x*(-2x) = 2x

c) 1/2y*3t*2y=1/2y*2y*3t=1/2y*2/1y*3t=2y*3t

d) -xy*(-xy) =-xy*xy=-xy²

Jak cos poplątałam to sorry ale mam nadzieję, że pomogłam

Suma miar kątów wewnętrznych trójkąta wynosi 180°.

Kąt wewnętrzny n-kąta foremnego ma miarę:  [tex]\frac{n - 2}{n} \cdot 180^o[/tex].

Przekątne wychodzące z jednego wierzchołka dzielą kat wielokąta foremnego na równe części, których miara wynosi:  [tex]\frac{180^o}{n}[/tex], gdzie n to liczba boków wielokąta.

----------

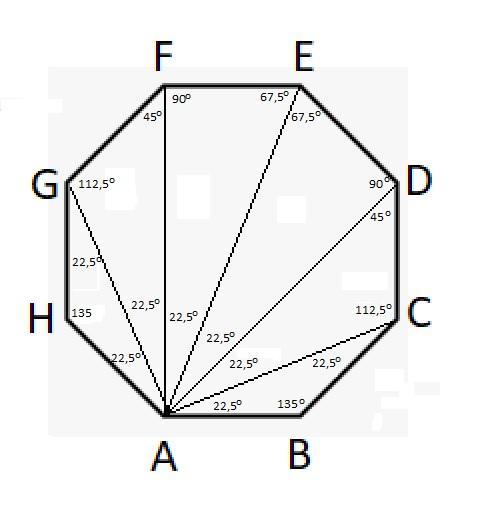
W ośmiokącie foremnym ABCDEFGH (rys. w zał.):

- miara kąta wewnętrzne wynosi: [tex]\frac{8 - 2}{\not{8}_2} \cdot \not{180^o}^{45^o}=\frac{\not{6}^3}{\not{2}_1} \cdot 45^o = 3\cdot 45^o = 135^o[/tex]

- miara kątów przy wierzchołku wyznaczonych przez przekątne:  [tex]\frac{180^o}{8}= 22,5^o[/tex]. (Miarę takich kątów możemy również obliczyć dzieląc miarę kąta wewnętrzne przez liczbę kątów utworzonych przez przekątne wychodzące z jednego wierzchołka:  [tex]\frac{135^o}{6}= 22,5^o[/tex]).

Zatem w każdym trójkącie wyznaczonym przez przekątne wychodzące z wierzchołka A, kąt przy wierzchołku A ma miarę 22,5°.

Miary kątów w trójkątach wyznaczonych przez przekątne wychodzące z wierzchołka A

ΔABC - trójkąt równoramienny (boki AB i BC to boki wielokąta foremnego). Zatem kąty przy podstawie AC mają równe miary.

|∡A| = |∡C| = 22,5°

|∡B| = 135° (jest to kąt wewnętrzny ośmiokąta foremnego)

Miary kątów w ΔABC: 22,5°; 135°; 22,5°

ΔACD

|∡A| = 22,5°

|∡C| = 135° - 22,5° = 112,5°

|∡D| = 180° - (22,5° + 112,5°) = 180° - 135° = 45°

Miary kątów w ΔABC: 22,5°; 112,5°; 45°

ΔADE

|∡A| = 22,5°

|∡D| = 135° - 45° = 90°

|∡E| = 180° - (22,5° + 90°) = 180° - 112,5° = 67,5°

Miary kątów w ΔABC: 22,5°; 90°; 67,5°

ΔAEF

|∡A| = 22,5°

|∡E| = 135° - 67,5° = 67,5°

|∡F| = 180° - (22,5° + 67,5°) = 180° - 90° = 90°

Miary kątów w ΔABC: 22,5°; 67,5°; 90°

ΔAFG

|∡A| = 22,5°

|∡C| = 135° - 90° = 45°

|∡D| = 180° - (22,5° + 45°) = 180° - 67,5° = 112,5°

Miary kątów w ΔABC: 22,5°; 45°; 112,5°

ΔAGH - trójkąt równoramienny (boki AH i HG to boki wielokąta foremnego). Zatem kąty przy podstawie AG mają równe miary.

|∡A| = |∡G| = 22,5°

|∡H| = 135° (jest to kąt wewnętrzny ośmiokąta foremnego)

Miary kątów w ΔABC: 22,5°; 22,5°; 135°

Odpowiedź:

1. TEZA: Lepiej jest mieć rodzeństwo niż być jedynakiem

1.Arg. : Rodzeństwo może pomóc w nauce

2.Arg. : Z rodzeństwem nigdy nie jest nudno, można grać razem w gry.

3.Arg. : Kiedy będziemy już dorośli będziemy mieli większą rodzinę, która będzie mogła nam pomóc.

2. TEZA : Warto się uczyć gramatyki.

1. Gramatyka pomaga nam się porozumiewać.

2. Dzięki temu gramatyce możemy dostać fajne oceny w szkole.

3. Dzięki gramatyce możemy w przyszłości otrzymać pracę humanistyczną.

3. TEZA : Prawdy moralne zawarte w baśniach i legendach są aktualne dla współczesnego człowieka.

1. Od zawsze ludzie posiadają takie same cechy, o których czesto jest mowa w baśniach i legendach.

2.W baśni o królewnę śnieżce zła królowa chciała być najpiękniejsza na świecie za wszelką cenę. W dzisiejszych czasach ludzie też dążą do, często mało istotnych, celów za wszelką cenę.

Odpowiedź:

Narnia

Szczegółowe wyjaśnienie:

B.5 1/3- 4 5/6=5 2/6- 4 5/6=3/6=1/2 litera I

C. 3 1/4- 2 5/8=3 2/8- 2 5/8= 5/8= litera M

D. 4 1/6 - 1 2/3= 4 1/6- 1 4/6= 3 7/6- 1 4/6= 2 1/2 litera G

6.

[tex]a) \ 2\frac{3}{4}-1\frac{1}{2}=2\frac{3}{4}-1\frac{2}{4} = 1\frac{1}{4}\\\\b) \ 5\frac{1}{3}-4\frac{5}{6} = 5\frac{2}{6}-4\frac{5}{6}=4\frac{8}{6}-4\frac{5}{6} = \frac{3}{6} = \frac{1}{2}\\\\c) \ 3\frac{1}{4}-2\frac{5}{8} = 3\frac{2}{8}-2\frac{5}{8} = 2\frac{10}{8}-2\frac{5}{8} = \frac{5}{8}\\\\d) \ 4\frac{1}{6}-1\frac{2}{3} = 3\frac{7}{6}-1\frac{4}{6} =2\frac{3}{6} = 2\frac{1}{2}[/tex]

hasło: NARNIA