zadanje 1 i 2 (Chiny i Japonia)proszę o szybkie rozwiązanie​

Odp A

Wyjaśnienie: 1kWh =3 600 000J

cena  energii elektrycznej  0,5zł/kWh

koszt 1GJ energii elektrycznej =0,5zł/kWh ·1GJ =0,5zł/kWh·1000000000J =

0,5zł/kWh ·(1000 000 000 :3 600 000)kWh =0,5zł/kWh ·277,8kWh =138,9zł

Odp A, GJ energii kosztuje około 139 zł

Odpowiedź:

a) odwaga:

Bohater: Antygona

Tytuł utworu "Antygona" Sofoklesa

Przykład sytuacji : Bracia Antygony, Eteokles i Polinejkes toczyli bratobójczą walkę o tron. Kreon uznał pierwszego za obrońcę ojczyzny, a drugiego za tchórza i zdrajcę ojczyzny.  Antygona naraziła się Kreonowi wypełniając swój rodzinny obowiązek, czyli pochowanie swojego brata Polinejkesa.  Kierowała się prawami boskimi. Za odwagę i za przeciwstawienie się rozkazowi Kreona zostaje skazana na śmierć. Została zamurowana w grobowcu i tam popełniła samobójstwo.

b) patriotyzm:

Bohater: Bernard Zygier

Tytuł utworu: " Syzyfowe prace " Żeromskiego

Przykład sytuacji : Na lekcji języka polskiego Zygier wyrecytował "Redutę Ordona. W wielu uczniach obudziły się uczucia patriotyczne. Marcin przeżył wstrząs, przypomniał sobie opowieść strzelca Nogi o powstańcach, zrozumiał, że szedł złą drogą. Żeromski opisuje młodzież, która za swój obowiązek wobec ojczyzny uważa: odmowę oglądania rosyjskich spektakli, protest wobec fałszowania polskiej historii, mówienie zakazanym językiem polskim.

Odpowiedź:

dzielniki liczby 24 = 2, 3, 4, 6, 8, 24

dzielniki liczby 36 = 2, 3, 4, 6, 9, 36

NWD(24,36) = 12

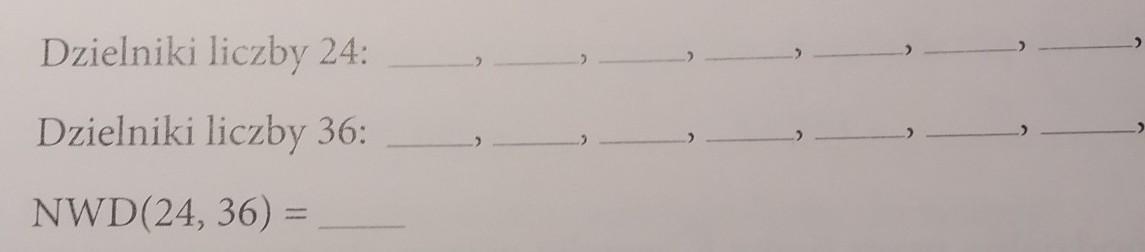
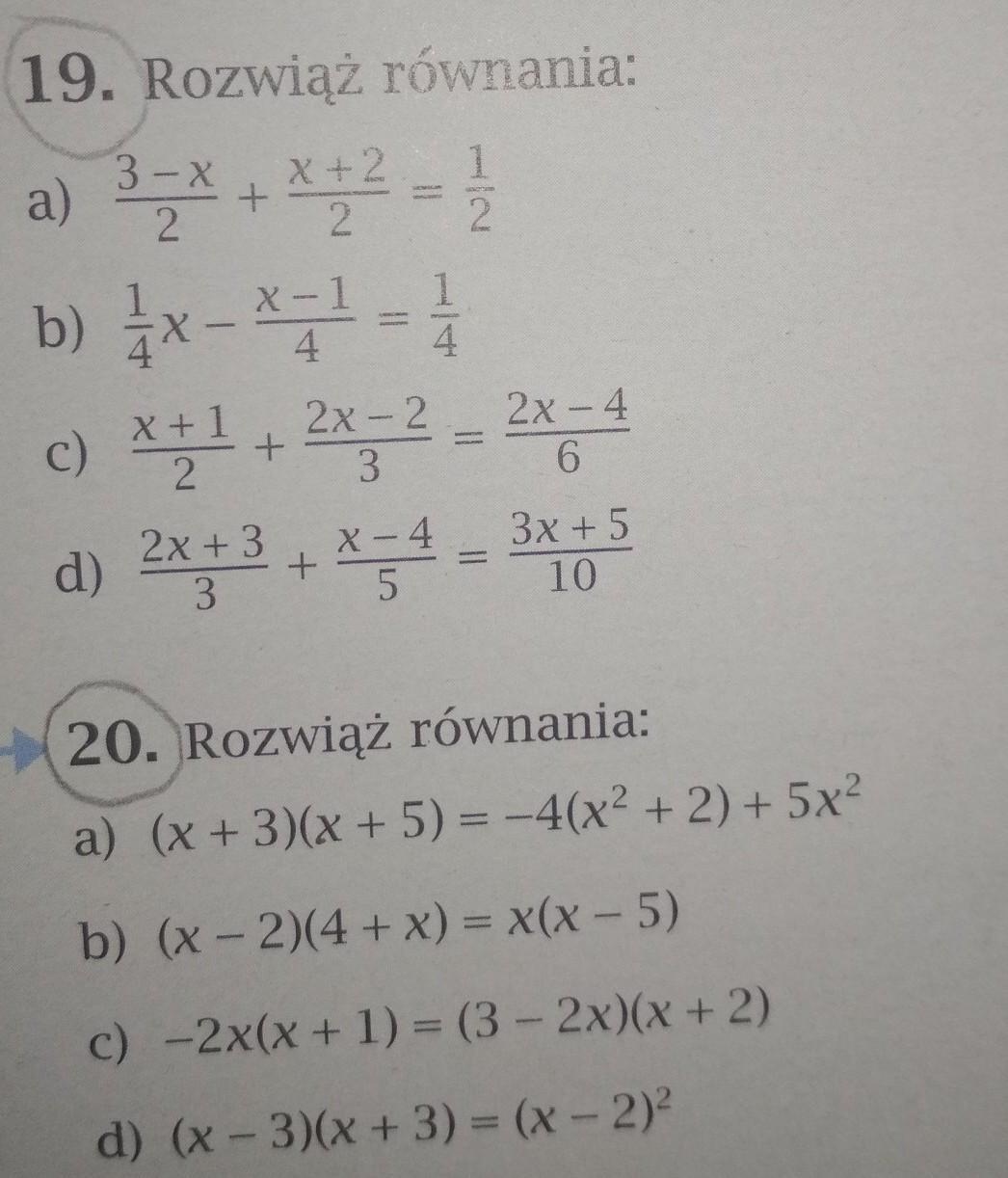Odpowiedź:

Zad. 19

[tex]a) \frac{3 - x}{2} + \frac{x + 2}{2} = \frac{1}{2} | \times 2 \\ 3 - x + x + 2 = 1 \\ 5 = 1 \\ [/tex]

wyrażenie nie ma rozwiązań

[tex]b) \frac{1}{4} x - \frac{x - 1}{4} = \frac{1}{4} | \times 4 \\ x - (x - 1) = 1 \\ x - x + 1 = 1 \\ 0 = 0[/tex]

wyrażenie należy do liczb rzeczywistych

[tex]c) \frac{x + 1}{2} + \frac{2x - 2}{3} = \frac{2x - 4}{6} | \times 6 \\ 3(x + 1) + 2(2x - 2) = 2x - 4 \\ 3x + 3 + 4x - 4 = 2x - 4 \\ 3x + 3 + 4x = 2x \\ 7x + 3 = 2x \\ 7x - 2x = - 3 \\ 5x = - 3 | \div 5 \\ x = - \frac{3}{5} [/tex]

[tex]d) \frac{2x + 3}{3} + \frac{x - 4}{5} = \frac{3x + 5}{10} | \times 30 \\ 10(2x + 3) + 6(x - 4) = 3(3x + 5) \\ 20x + 30 + 6x - 24 = 9x + 15 \\ 26x + 6 = 9x + 15 \\ 26x - 9x = 15 - 6 \\ 17x = 9 | \div 17 \\ x = \frac{9}{17} [/tex]

Zad. 20

[tex]a)(x + 3)(x + 5) = - 4( {x}^{2} + 2) + 5 {x}^{2} \\ {x}^{2} + 5x + 3x + 15 = - 4 {x}^{2} - 8 + 5 {x}^{2} \\ {x}^{2} + 8x + 15 = {x}^{2} - 8 \\ 8x = - 8 - 15 \\ 8x = - 23 | \div 8 \\ x = - \frac{23}{8} = - 2 \frac{7}{8} [/tex]

[tex]b)(x - 2)(4 + x) = x(x - 5) \\ 4x + {x}^{2} - 8 - 2x = {x}^{2} - 5x \\ 4x - 8 - 2x = - 5x \\ 2x - 8 = - 5x \\ 2x + 5x = 8 \\ 7x = 8 | \div 7 \\ x = \frac{8}{7} [/tex]

[tex]c) - 2x(x + 1) = (3 - 2x)(x + 2) \\ - 2 {x}^{2} - 2x = 3x + 6 - 2 {x}^{2} - 4x \\ - 2x = 3x + 6 - 4x \\ - 2x = - x + 6 \\ - 2x + x = 6 \\ - x = 6 \\ x = - 6[/tex]

[tex]d)(x - 3)(x + 3) = (x - 2 {)}^{2} \\ {x}^{2} - 9 = {x}^{2} - 4x + 4 \\ - 9 = - 4x + 4 \\ 4x = 4 + 9 \\ 4x = 13 | \div 4\\ x = \frac{13}{4} = 3 \frac{1}{4} [/tex]

Odpowiedź:

Szczegółowe wyjaśnienie: