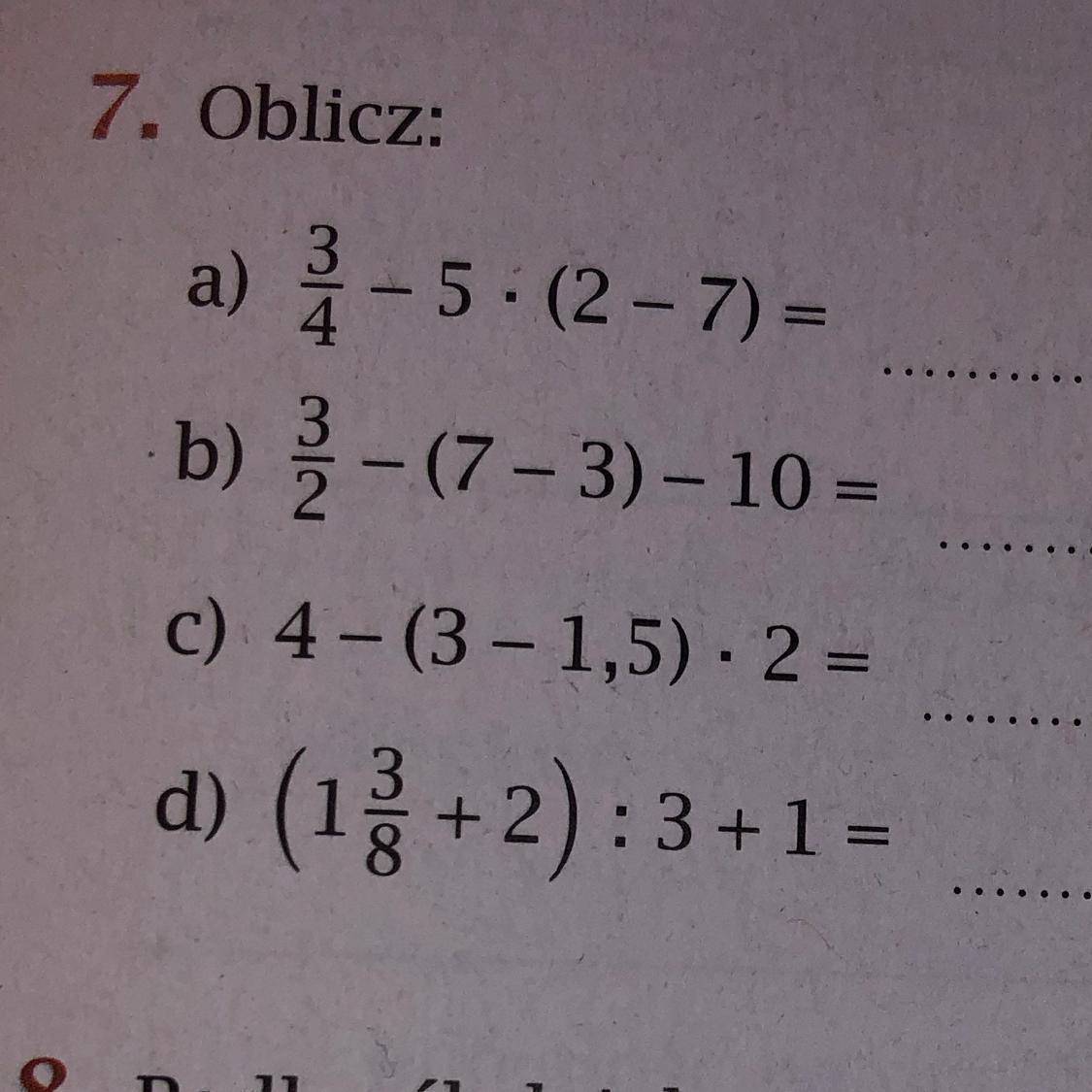B. opiaE3 Przyporządkuj wymienionym poniżej postaciom właściwe opisy.A. Ludwik Mierosławski,B. Edward Dembowski, C. Jakub Szela,1. Organizator powstania krakowskiego. Zginął 27 lutego 1846 r., gdy wojska austriackieostrzelały procesję patriotyczną, której przewodził.2. Przywódca wystąpien rewolucyjnych w Wielkopolsce. Po upadku tamtejszego powstaniadostał się do niewoli, lecz na prośbę rządu francuskiego został zwolniony.3. Przywódca chłopów w czasie rabacji galicyjskiej. Stał się na dziesięciolecia postrachempolskiej szlachty.24plls szybko to ważne kl 7

Odpowiedzi 1
Wyjaśnienie: A-2, B- 1, C- 3
A. Ludwik Mierosławski- 2. Przywódca wystąpień rewolucyjnych w Wielkopolsce. Po upadku tamtejszego powstania dostał się do niewoli, lecz na prośbę rządu francuskiego został zwolniony.
B. Edward Dembowski- 1. Organizator powstania krakowskiego. Zginął 27 lutego 1846 r., gdy wojska austriackie ostrzelały procesję patriotyczną, której przewodził.
C. Jakub Szela- 3. Przywódca chłopów w czasie rabacji galicyjskiej. Stał się na dziesięciolecia postrachem polskiej szlachty.
-
Autor:
riyangac
-
Oceń odpowiedź:
1
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years