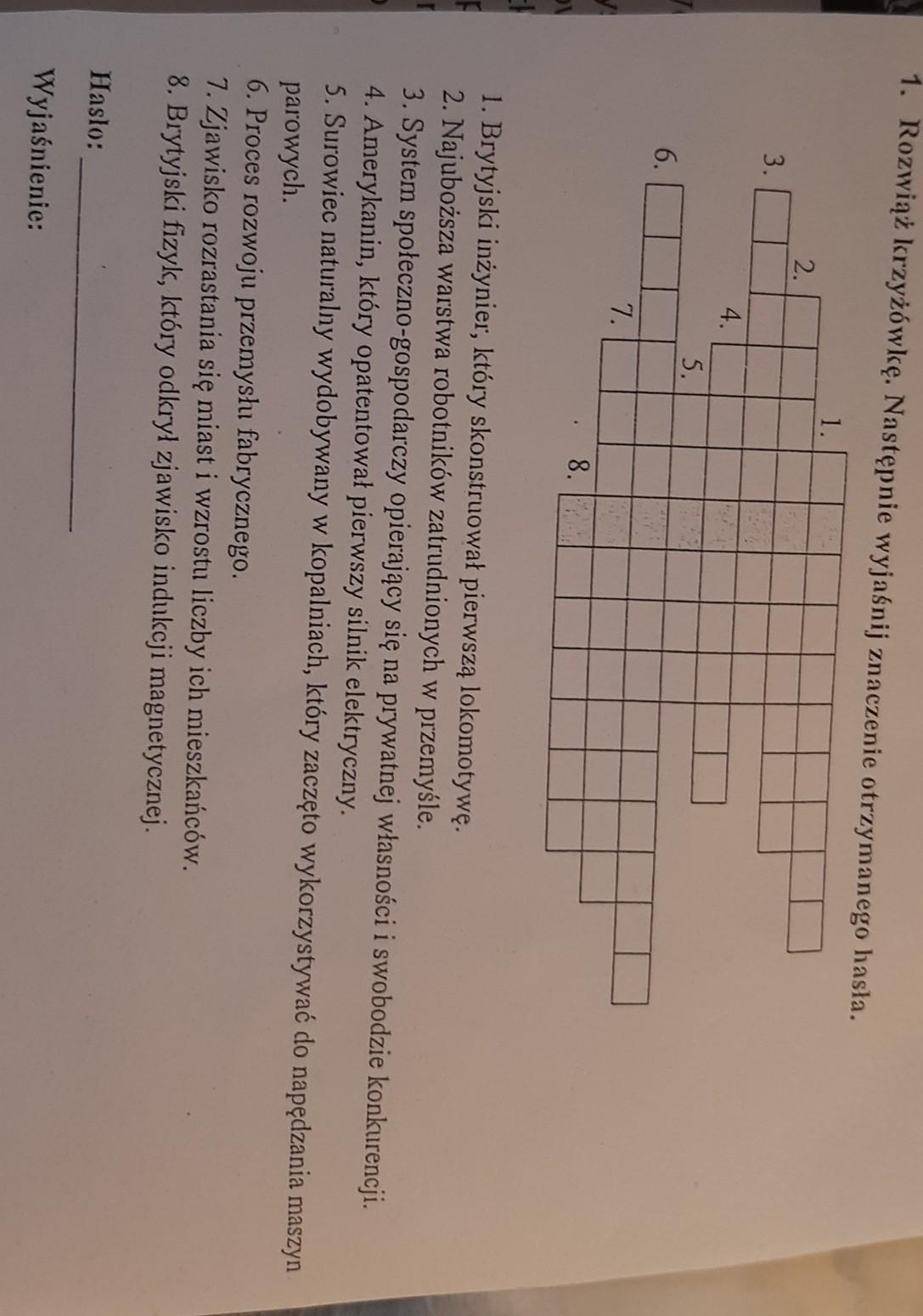
1.2. Rewolucja przemysłowa1. Rozwiąż krzyżówkę. Następnie wyjaśnij znaczenie otrzymanego lasla.2.3.6.S.C7.P81. Brytyjski inżynier, który skonstruował pierwszą lokomotywę.2. Najuboższa warstwa robotników zatrudnionych w przemyśle3. System spoleczno-gospodarczy opierający się na prywatnej własności i swobodzie konkurencji.4. Anierykanin, który opatentował pierwszy silnik elektryczny.5. Surowiec naturalny wydobywany w kopalniach, który zaczęto wykorzystywać do napędzania maszynparowych.6. Proces rozwoju przemysłu fabrycznego.7. Zjawisko rozrastania się miast i wzrostu liczby ich mieszkańców.8. Brytyjski fizyk, który odkryl zjawisko indukcji magnetycznejHaslo:Wyjaśnienie:
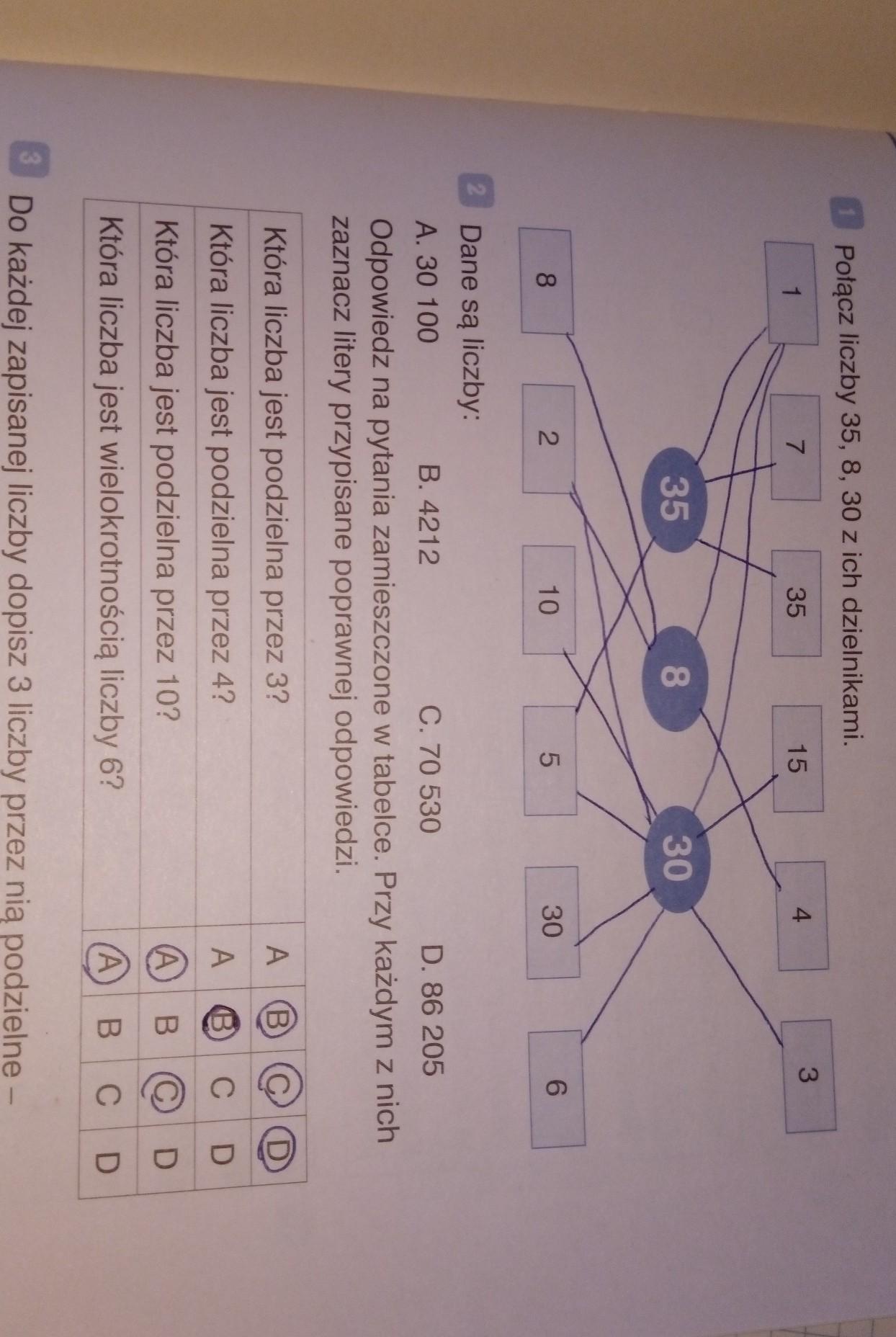
Odpowiedzi 1
Odpowiedź:
Rozwiązanie w załączniku:
Wyjaśnienie:

-
Autor:
armanidbcr
-
Oceń odpowiedź:
1
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years