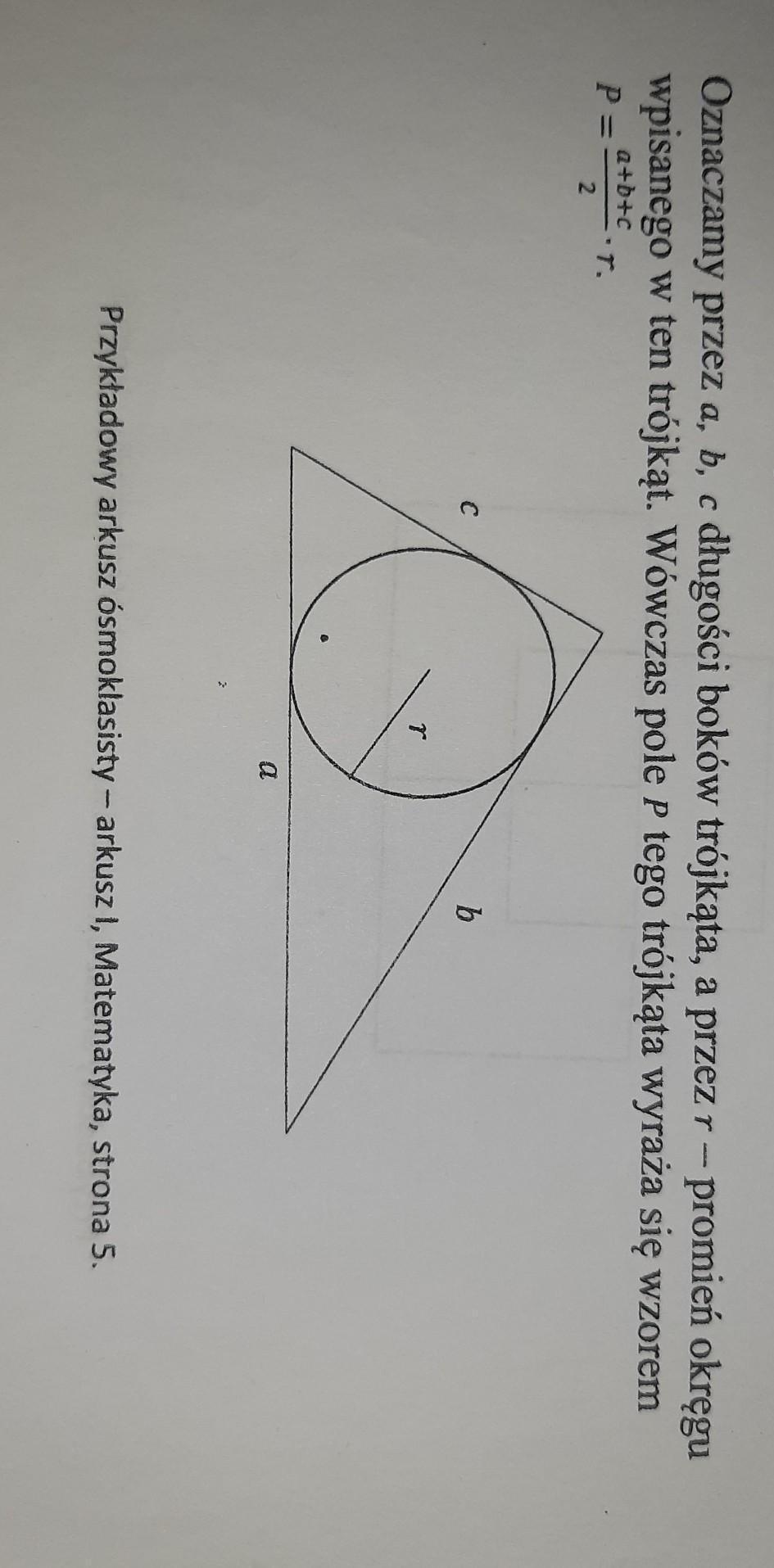
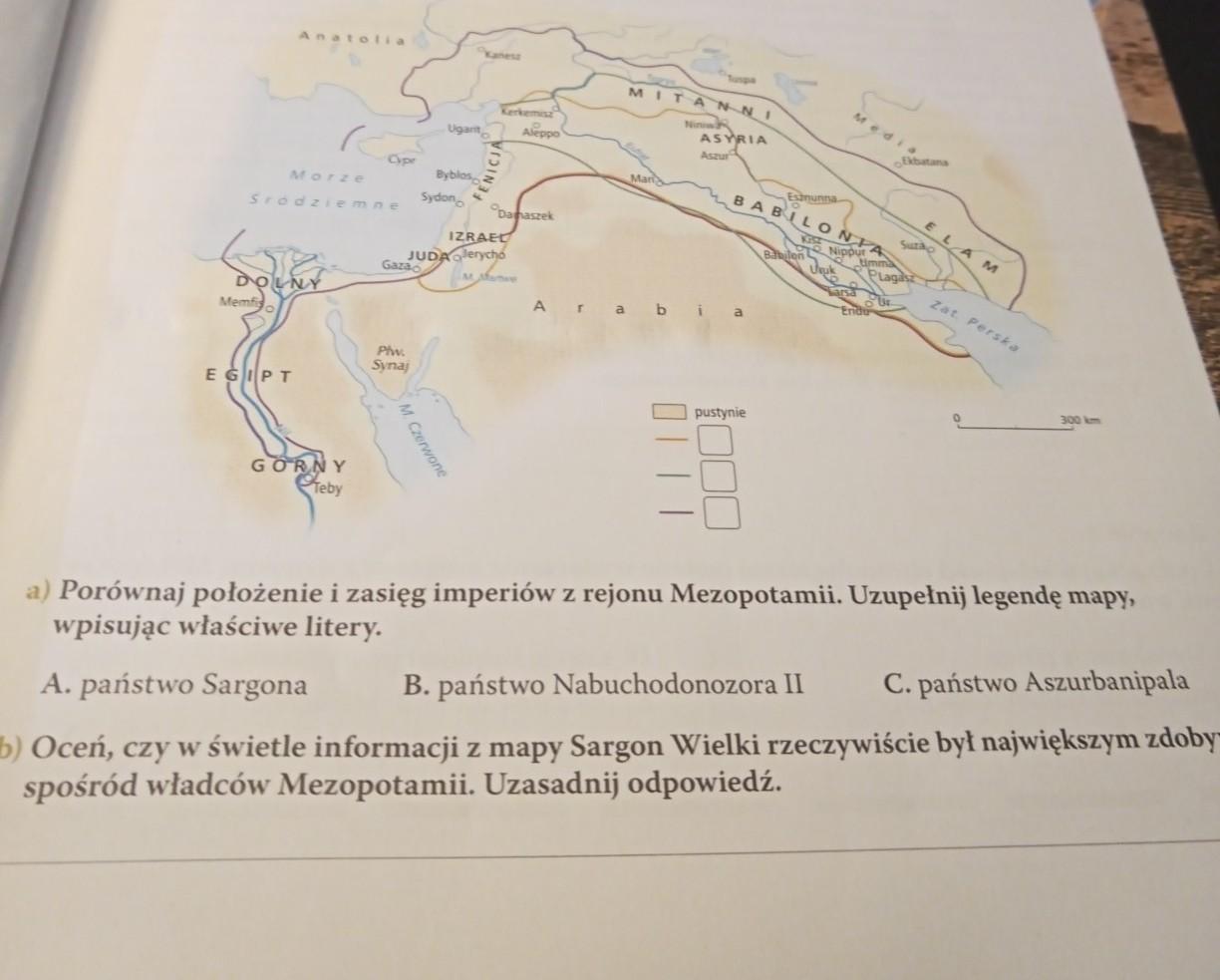
Ktoś pomoże? a) Porównaj położenie i zasięg imperiów z rejonu Mezopotamii. Uzupełnij legendę mapy, wpisując właściwe litery. A. państwo Sargona B. państwo Nabuchodonozora II C. państwo Aszurbanipala ​

Odpowiedź:

Ten jubilat ma obecnie 55 lat.

Szczegółowe wyjaśnienie:

x = obecny wiek jubilata

Układam równanie:

(x - 27) * (x + 15) = 2015 - x

x² + 15x - 27x - 405 = 2015 - x

x² - 12x - 405 - 2015 + x = 0

x² - 11x - 2420 = 0

Obliczam deltę i pierwiastki :

a = 1 ,b = - 11 , c = - 2420

∆ = b² - 4ac

∆ = (- 11)² - 4 * 1 * (-2420) = 121 + 9680 = 9801

√∆ = 99

x1 = (-b -√∆)/2a

x1 = (11 - 99)/2 = -88/2 = - 44

Ta wartość odpada, ponieważ wiek jubilata nie może być liczbą ujemną.

x2 = (-b + √∆)/2a

x2 = (11 + 99)/2 = 110/2 = 55

Więc ten jubilat ma obecnie 55 lat.

Witaj :)

Mamy dany wzór wyjściowy:

[tex]\Large \boxed{P=\frac{a+b+c}{2}\cdot r}[/tex]

Naszym zadaniem jest tak przekształcić powyższy wzór, aby można było z niego wyliczyć promień okręgu wpisanego w trójkąt.

• Mnożę obustronnie przez mianownik ułamka znajdującego się po prawej  stronie wzoru. Dzięki temu pozbędziemy się liczby 2 w ułamku:

[tex]2P=(a+b+c)\cdot r[/tex]

• Dzielę obustronnie przez (a+b+c). Dzięki temu od razu wyznaczymy wzór na promień okręgu opisanego.

[tex]\frac{2P}{a+b+c}=r[/tex]

Ostatecznie nasz wzór wygląda następująco:

[tex]\Large \boxed{r=\frac{2P}{a+b+c} }[/tex]

W tym przypadku dzieliliśmy przez niewiadome (a+b+c), w takim wypadku należy zastosować odpowiednie założenia, że suma boków nie może dać w wyniku 0. W tej sytuacji nigdy tak nie będzie, bo żaden z boków trójkąta nie może mieć długości 0, ani wartości ujemnej.

ODP.: C.

At the age of eight, she began attending singing lessons and soon joined the parish children's choir. She was a member of the hip-hop dance group R-Revolution. She likes to listen to rap, among her favorite songs is the red carpet and Without fear of the big toe. In his spare time, he spends time with his family and makes up for school. Before she began seriously singing, she trained rhythmic gymnastics, ballroom dancing and judo. Together with the clothing brand "reporter Young", she created a collection of Roxie clothes. On June 7, 2019, she released her debut album "Roksana Węgiel" After 38 days, she achieved the status of a gold record.Roxie's favorite cake is cheesecake, she loves dogs. I like her and I wish you a lot of success in your career.

Mam nadzieję, że jest dobrze i że pomogłam!<33 Liczę na najj <33

-Flaureyy :))

a)

Obwod: 2*8a+2*3c=16a+6c

Pole: 8a*3c=24ac

b)

Obwod: 2*7+2*(2x+3)=14+4x+6=4x+20

Pole: 7*(2x+3)=14x+21

c)

Obwod: 2*3a+2*(7a+1)=6a+14a+2=20a+2

Pole: 3a*(7a+1)=21a²+3a

d)

Obwod: 2*(a-3)+2*2b=2a-6+4b=6a+6

Pole: 2b*(a-3)=2ab-6b

Odpowiedź:

Mam nadzieję że się doczytasz