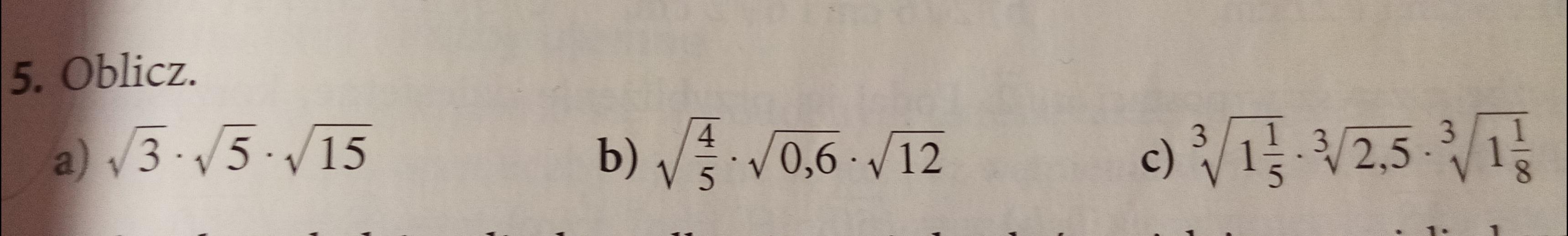Podaj skutki rewolucji kulturalnej przeprowadzonej w Chinachpodręcznik wczoraj i dziś nowa era!potrzebuje na już​

Odpowiedź:

V - objętość ostrosłupa  = 1/3 * 6  cm * 4  cm * 3 cm = 24 cm³

V₁ - objętość graniastosłupa = 6 cm * 4 cm * 3  cm  = 72 cm³

V₁/V₂ =  72 cm³ : 24 cm³ = 3 razy

Graniastosłup ma większą objętość

Objętość graniastosłupa jest trzy razy większa

Zad.3

- wydzielanie się do atmosfery CO2 niekorzystnie wpływa na klimat i przyczynia się do tzw. efektu cieplarnianego

- częściowe lub całkowite zniszczenie roślin ( np. korony drzew, pnie, korzenie oraz młode drzewostany) i organizmów znajdujących się w glebie, narusza to piętro producentów w biocenozie

- w ogni giną lub ulegają silnym poparzeniom zwierzęta ( ssaki, ptaki, płazy, gady i bezkręgowce) zamieszkujące dany obszar,

- ogień niszczy ich siedliska i miejsca lęgowe,

- zniszczeniu i degradacji ulega również gleba, pożar niszczy jej mikroflorę

Zad.4

Odp. B, D

wyjaśnienie:

Wilgotne powietrze równikowe unosząc się ulega ochłodzeniu.

Odpowiedź:

W załaczniku

Szczegółowe wyjaśnienie:

[tex]a)\ \sqrt3\cdot\sqrt5\cdot\sqrt{15}=\sqrt{3\cdot5\cdot15}=\sqrt{15\cdot15}=\sqrt{15^2}=15\\\\b)\ \sqrt{\dfrac{4}{5}}\cdot\sqrt{0,6}\cdot\sqrt{12}=\sqrt{\dfrac{4}{5}\cdot\dfrac{6}{10\!\!\!\!\!\diagup_5}\cdot12\!\!\!\!\!\diagup^6}=\sqrt{\dfrac{4\cdot6^2}{5^2}}=\dfrac{\sqrt4\cdot\sqrt{6^2}}{\sqrt{5^2}}=\dfrac{2\cdot6}{5}=\dfrac{12}{5}[/tex]

[tex]c)\ \sqrt[3]{1\dfrac{1}{5}}\cdot\sqrt[3]{2,5}\cdot\sqrt[3]{1\dfrac{1}{8}}=\sqrt[3]{\dfrac{6\!\!\!\!\diagup^3}{5\!\!\!\!\diagup_1}\cdot\dfrac{25\!\!\!\!\!\diagup^{5\!\!\!\!\diagup^1}}{10\!\!\!\!\!\diagup_2}\cdot\dfrac{9}{8\!\!\!\!\diagup_4}}=\sqrt[3]{\dfrac{27}{8}}=\dfrac{\sqrt[3]{27}}{\sqrt[3]8}=\dfrac{3}{2}[/tex]

skorzystałem z definicji pierwiastka:

[tex]\sqrt{a}=b\iff b^2=a,\ \text{gdzie}\ a,b\geq0\\\\\sqrt[3]{a}=b\iff b^3=a[/tex]

oraz z twierdzeń dotyczących działań na pierwiastkach:

[tex]\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b},\ \text{gdzie}\ a,b\geq0\\\\\sqrt[3]{a\cdot b}=\sqrt[3]{a}\cdot\sqrt[3]b\\\\\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}},\ \text{gdzie}\ a\geq0\ \wedge\ b>0\\\\\sqrt[3]{\dfrac{a}{b}}=\dfrac{\sqrt[3]{a}}{\sqrt[3]{b}},\ \text{gdzie}\ b\neq0\\\\\sqrt{a^2}=a,\ \text{gdzie}\ a\geq0[/tex]