Podaj dwie przyczyny wprowadzenia przez peryklesa reformy sądownictwa w atenach.

Dialog z wykorzystaniem związku frazeologicznego ,,nić Ariadny''.

— Czy rozwiązałeś już problem związany z anulowaniem rezerwacji lotu?

— Tak, ale zajęło mi to dużo czasu. Początkowo próbowałem sam się tym zająć, ale modyfikacja planu lotów okazała się być bardzo skomplikowana.

— Czy mogłeś liczyć na czyjąś pomoc?

— Tak, ostatecznie to rozmowa z asystentem z działu obsługi klienta okazała się być nicią Ariadny.

• Związek frazeologiczny nić Ariadny oznacza otrzymaną pomoc, wskazówki, które ukażą rozwiązanie łamigłówki, problemu.

• Wyrażenie to nawiązuje do mitologii greckiej i mitu, w którym to Ariadna podarowała Tezeuszowi kłębek nici, by mógł on wydostać się z labiryntu.

#SPJ4

Prośba Priama o zwrócenie ciała jego syna poległego w walce z Achillesem wywołała u słynnego wojownika uczucie współczucia, szacunku i zrozumienia.

Najprawdopodobniej powodem tych uczuć był fakt, że Achilles sam stracił swojego najlepszego przyjaciela Partoklosa, a także uczucie do jego własnego ojca, którego wspomnienie przywołał Priam. Widząc ojcowską miłość Priama, wzruszył się, przypomniał sobie własnego rodzica i zrozumiał ogrom jego cierpienia. Nie tylko oddał zwłoki Hektora, ale też obmył je i ułożył w łożu pogrzebowym. Achilles, widząc, że nawet tak potężny człowiek, jak Priam staje się mu uległy, stwierdził, że musi przeżywać on niewiarygodne cierpienie.

O czym opowiada Iliada?

Iliada opowiada o ostatnich dniach wojny trojańskiej. Opisuje historię Achillesa i jego kolejne potyczki, w tym zabicie Hektora, syna Priama. W Iliadzie ludzkie historie spotykają się z losami bogów.

#SPJ4

Witaj :)

  Naszym zadaniem jest wyjaśnić, dlaczego helowce w warunkach normalnych nie występują w postaci cząsteczek dwuatomowych.

  Jak wiemy, każdy pierwiastek chemiczny dąży do tego, aby posiadać trwałą konfigurację elektronową. Pierwiastki dążą do tego, aby posiadać na ostatniej powłoce (powłoce walencyjnej) osiem, lub dwa elektrony. Jest to tzw. Reguła oktetu (lub dubletu), lub reguła helowca. Reguła oktetu mówi o tym, że pierwiastki chemiczne dążą do uzyskania ośmiu elektronów na powłoce walencyjnej, czyli do konfiguracji najbliższego dla nich gazu szlachetnego. Dla reguły dubletu pierwiastki dążą do uzyskania dwóch elektronów na powłoce walencyjnej (konfiguracji helu). Jeżeli spojrzymy na układ okresowy pierwiastków, zauważamy, że gazy szlachetne (helowce) znajdują się w 18 grupie, czyli na ostatniej powłoce posiadają 18-10=8 elektronów walencyjnych (z wyjątkiem helu, który ma 2 elektrony walencyjne). Pierwiastki te posiadają trwałą konfigurację powłoki walencyjnej, mają oktet albo dublet (dla helu). Niekorzystnie byłoby dla nich oddać lub przyjąć elektrony, więc nie mają możliwości tworzenia cząsteczek dwuatomowych.

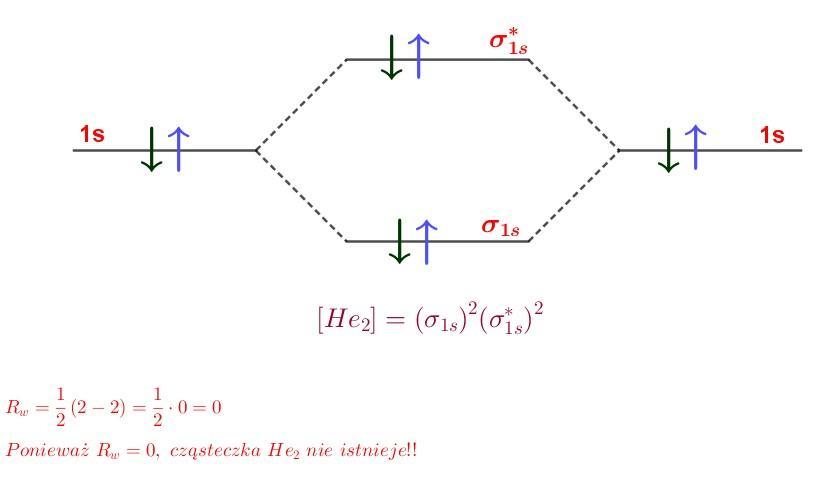
  Drugim dokładniejszym sposobem na wytłumaczenie tego, że gazy szlachetne (helowce) nie tworzą cząsteczek dwuatomowych, jest zastosowanie teorii orbitali molekularnych. W załączniku znajduje się diagram energetyczny dla cząsteczki dwuatomowej helu. Jak wiemy, atom helu posiada 2 elektrony walencyjne, ale mamy cząsteczkę dwuatomową, więc tych elektronów będzie 2 razy więcej, czyli 4. W najniższym miejscu diagramu mamy orbital wiążący [tex]\sigma_{1s}[/tex]. Na tym orbitalu mogą znaleźć się 2 elektrony o przeciwnych spinach. Na samej górze mamy orbital antywiążący [tex]\sigma^*_{1s}[/tex]. Na tym orbitalu mogą znaleźć się również 2 elektrony. Parametrem, który opisuje, czy dana cząsteczka może istnieć, jest tzw. rząd wiązania. Rząd wiązania jest połową różnicy między ilością elektronów na orbitalu wiążącym a ilością elektronów na orbitalu antywiążącym. Możemy to wyrazić wzorem:

                                       [tex]\Large \boxed{R_w=\frac{1}{2}\Big(n_e-n^*_e\Big) }[/tex]

gdzie:

[tex]n_e\ - \ ilosc\ elektronow\ na\ orbitalu\ wiazacym\\n^*_e\ - \ ilosc\ elektronow\ na\ orbitalu\ antywiazacym[/tex]

W naszym przypadku mamy:

[tex]n_e=2\\n^*_e=2[/tex]

Więc rząd wiązania wynosi:

[tex]\Large \boxed{R_w=\frac{1}{2}\cdot(2-2)=\frac{1}{2}\cdot 0=0\implies He_2\ nie\ istnieje }[/tex]

Analogicznie możemy postąpić dla innych gazów szlachetnych, co potwierdza, że nie występują one w postaci cząsteczek dwuatomowych.

W załączniku diagram energetyczny dla cząsteczki helu.

Poniżej znajdują się zapisane w punktach zasady, którymi zdaniem Jana Kochanowskiego człowiek powinien się kierować w życiu aby być zadowolony i szczęśliwy na podstawie treści pieśni drugiej.

W pieśni drugiej Jan Kochanowski pokazuje, że żeby być szczęśliwym należy:

• sumiennie pracować i być dumny ze swojej uczciwości
• kontemplować przyrodę i zachwycać się jej pięknem
• Nie kłócić się z ludźmi i unikać negatywnych odczuć wobec innych
• Dużo czasu spędzać wokół innych osób

Tego typu analizy poezji, wymagają odtworzenia emocji, które się wyzwalają w nas podczas czytania i w jaki sposób zostały one wywołane.

#SPJ4