Polska w XIII-XV wiekukładzie dokonania króla w każdej z podanych dziedzin.Uzupełnij tabelę przedstawiającą zasługi Kazimierza Wielkiego. Wpisz po jednym przy-Dokonania Kazimierza WielkiegoDziedzinaPolitykaNaukaGospodarkaObronnośćOceń, czy poniższe zdania są prawdziwe. Zaznacz literę „P” przy zdaniach prawdziwych,a „F”- przy fałszywych.Na początku panowania Kazimierza Wielkiego Polska utrzymywałaPFprzyjazne stosunki tylko z państwem zakonu krzyżackiego. .Kazimierz Wielki prowadził pokojową politykę w relacjach z sąsiadami.PFUtworzenie Akademii Krakowskiej przyczyniło się do usprawnieniaP Ffunkcjonowania polskiego państwa.Po śmierci Kazimierza Wielkiego władzę w Polsce przejął jego syn.PTo zostaw.DAJE PUNKTY I NAJLEPDZA ODPOWIEDZ !!! ​

Odpowiedź:

wzrok, oczy

smak, kubki smakowe

węch, nos

słuch, ucho

plamka- miejsce o największej rozdzielczości widzenia

błona-chyba chodzi o naczyniówkę

Promienie świetlne przedostają się do oka przez rogówkę (A). Zostają one odpowiednio załamane dzięki soczewce (D). Obraz powstający w siatkówce jest odwrócony i pomniejszony (E). Mózg odbiera informacje płynące z obu oczu,nakłada je na siebie i dzięki temu widzimy obraz trójwymiarowy (H)

Wyjaśnienie:

Odpowiedź:

na pewno kosci wypełnione powietrzrm i konczyny przekształcone w skrzydla

Odpowiedź:

kości wypełnione powietrzem

kończyny przekształcone w skrzydła

obecność powiek

Odpowiedź:

A=1,84

B=4,692

Szczegółowe wyjaśnienie:

Odpowiedź:

tak mi to wychodzi

A=4,594

B= 4,602

Odpowiedź:

[tex]a)~~L=(14+2\sqrt{5} )~~[j],~~P_{trapez} =18~[j^{2}][/tex]

[tex]b)~~L=(5\sqrt{2}+\sqrt{34} +2\sqrt{13})~[j] ,~~P_{\Delta ABC} =19~[j^{2}][/tex]

[tex]c)~~L=4\sqrt{13} ~[j ],~~P_{romb} =5~[j^{2}][/tex]

Szczegółowe wyjaśnienie:

Korzystamy ze wzorów:

• długość odcinka o końcach w punktach [tex]A(x_{a} ,y_{a} ),~~B(x_{b} ,y_{b} )[/tex]  jest dana wzorem  [tex]\mid AB \mid=\sqrt{(x_{b} -x_{a} )^{2} +(y_{b} -y_{a} )^{2} }[/tex]
• wzór na pole trapezu  [tex]P=\dfrac{a+b}{2} \cdot h, ~~gdzie ~~a,b~~-~~podstawy ~~trapezu, ~~h-~~wysokosc~~trapezu[/tex]
• wzór na pole trójkąta  [tex]P=\dfrac{a\cdot h}{2} ,~~gdzie ~~h~~-~~wysokosc~~poprowadzona ~~do~~podstawy~~a[/tex]
• wzór na pole prostokąta  [tex]P=a\cdot b,~~gdzie ~~a,b~~-~~dlugosci~~dwoch~~sasiednich~~bokow[/tex]
• wzór na pole rombu  [tex]P=\dfrac{e\cdot f}{2},~~gdzie~~e,f~~-~~dlugosci ~~przekatnych~~rombu[/tex]

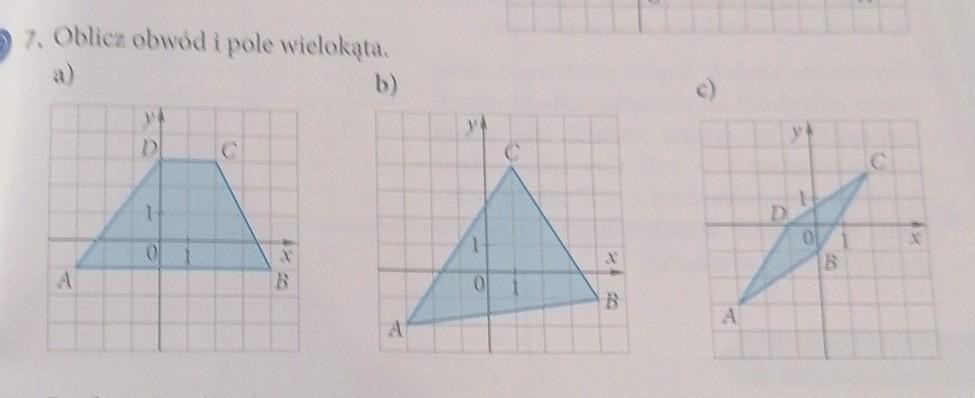
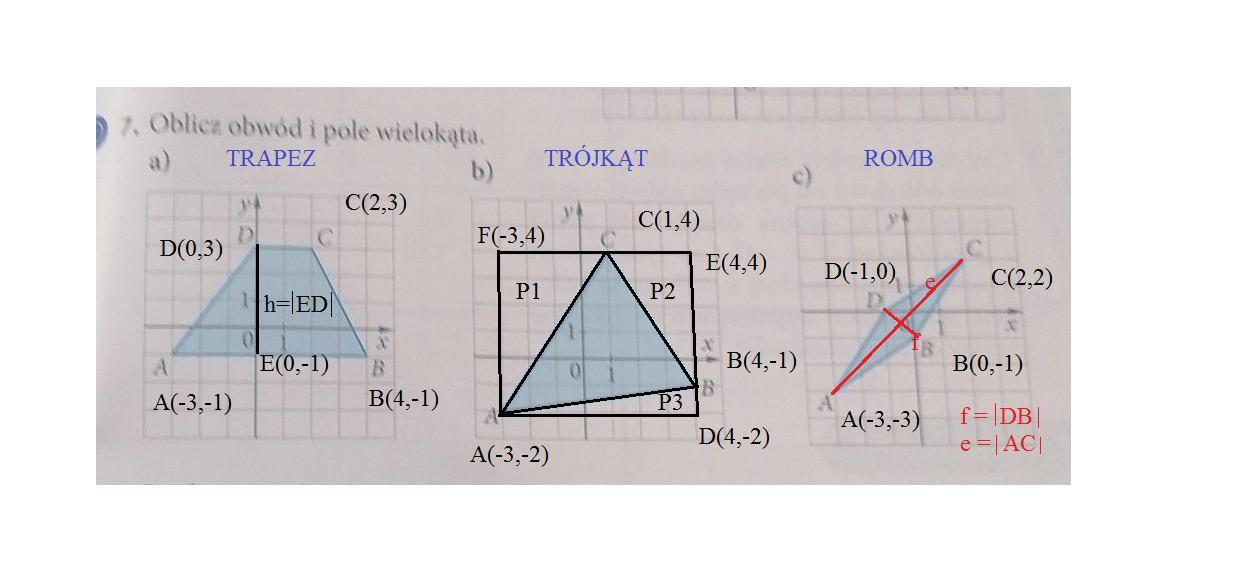
Rysunek w załączniku.

[tex]\boxed{a}[/tex]

Obliczamy długości boków trapezu oraz jego wysokość.

[tex]A(-3,-1),~~B(4,-1),~~C(2,3),~~D(0,3),~~E(0,-1)\\\\\mid AB \mid =\sqrt{[4-(-3)]^{2} +[-1-(-1)]^{2} } =\sqrt{49+0} =\sqrt{7^{2} } =7\\\\\mid BC \mid =\sqrt{(2-4)^{2} +[3-(-1)]^{2} } =\sqrt{4+16}=\sqrt{20} =2\sqrt{5} \\\\\mid CD \mid =\sqrt{(0-2)^{2} +(3-3)^{2} } =\sqrt{4+0} =\sqrt{2^{2} } =2\\\\\mid AD \mid =\sqrt{[0-(-3)]^{2} +[3-(-1)]^{2} } =\sqrt{9+16} =\sqrt{25} =\sqrt{5^{2} } =5\\\\h= \mid ED \mid =\sqrt{(0-0)^{2} +[3-(-1)]^{2} } =\sqrt{16} =\sqrt{4^{2} } =4[/tex]

Obliczamy obwód trapezu.

[tex]L=\mid AB \mid +\mid BC \mid +\mid CD \mid +\mid AD \mid \\\\L=7+2\sqrt{5} +2+5\\\\\boxed{L=(14+2\sqrt{5} )~~[j]}[/tex]

Obliczamy pole trapezu.

[tex]P_{trapez} =\dfrac{(\mid AB\mid+\mid CD\mid )}{2} \cdot h\\\\ P_{trapez} =\dfrac{(7+2)}{2} \cdot 4\\\\\boxed{ P_{trapez} =18~[j^{2}]}[/tex]

[tex]\boxed{b}[/tex]

Obliczamy długości boków trójkąta.

[tex]\mid AB\mid =\sqrt{[4-(-3)]^{2} +[-1-(-2)]^{2} } =\sqrt{49+1} =\sqrt{50} =\sqrt{5^{2} \cdot 2} =5\sqrt{2} \\\\\mid BC\mid=\sqrt{(1-4)^{2} +[4-(-1)]^{2} } =\sqrt{9+25} =\sqrt{34} \\\\\mid AC\mid=\sqrt{(-3-1)^{2} +(-2-4)^{2} } =\sqrt{16+36}=\sqrt{52} =\sqrt{4\cdot 13} =2\sqrt{13}[/tex]

Obliczamy obwód trójkąta.

[tex]L=\mid AB\mid+\mid BC\mid+\mid AC\mid\\\\\boxed{L=(5\sqrt{2}+\sqrt{34} +2\sqrt{13} )~[j] }[/tex]

Obliczamy pole trójkąta.

Aby obliczyć pole trójkąta, w pierwszej kolejności obliczamy długości sąsiednich boków prostokąta oraz długości boków trójkątów potrzebnych do obliczenia ich pól ( P₁, P₂, P₃ ).

[tex]I.\\\\\mid AD\mid=\sqrt{[4-(-3)]^{2} +[-2-(-2)]^{2} } =\sqrt{7^{2} }=7\\ \\\mid DB\mid=\sqrt{(4-4)^{2} +[-1-(-2)]^{2} } =\sqrt{1} =1\\\\P_{3} =\dfrac{\mid AD\mid\cdot \mid DB\mid }{2} \\\\\boxed{P_{3} =\dfrac{7\cdot 1}{2} =3,5~[j^{2} ]}\\\\II.\\\\\mid AF\mid = \sqrt{[-3-(-3)]^{2} +[4-(-2)]^{2} } =\sqrt{6^{2} } =6\\\\\mid CF\mid =\sqrt{(-3-1)^{2} +(4-4)^{2} } =\sqrt{4^{2} } =4\\\\P_{1} =\dfrac{\mid AF\mid\cdot \mid CF\mid }{2}\\\\\boxed{P_{1} =\dfrac{6\cdot 4}{2} =12~[j^{2} ]}[/tex]

[tex]III.\\\\\mid AD \mid=7\\\mid AF\mid =6\\\\\boxed{P_{prostokat} =6\cdot 7=42~[j^{2} ]}[/tex]

[tex]IV.\\\\\mid BE\mid =\sqrt{(4-4)^{2} +[4-(-1)]^{2} } =\sqrt{5^{2} }=5 \\\\\mid EC\mid =\sqrt{(1-4)^{2} +(4-4)^{2} } =\sqrt{3^{2} } =3\\\\P_{2} =\dfrac{\mid BE\mid \cdot \mid EC\mid }{2} \\\\\boxed{P_{2} =\dfrac{5\cdot 3}{2} =7,5~[j^{2} ]}[/tex]

teraz obliczamy pole trójkąta.

[tex]P_{\Delta ABC} =P_{prostokat} -P_{1} -P_{2} -P_{3} \\\\P_{\Delta ABC} =42-12-7,5-3,5\\\\\boxed{P_{\Delta ABC} =19~[j^{2}] }[/tex]

[tex]\boxed{ c} }[/tex]

Obliczamy długości boków rombu.

[tex]\mid AB\mid = \mid BC\mid=\mid CD\mid = \mid AD\mid\\\\\mia AB\mid = \sqrt{[0-(-3)]^{2} +[-1-(-3)]^{2} } =\sqrt{9+4} =\sqrt{13}[/tex]

Obliczamy obwód rombu.

[tex]L=4\cdot \mid AB\mid \\\\L=4\cdot \sqrt{13} \\\\\boxed{L=4\sqrt{13} ~[j ]}[/tex]

Obliczamy długości przekątnych rombu.

[tex]f=\mid BD\mid = \sqrt{(-1-0)^{2} +[0-(-1)]^{2} } =\sqrt{1+1} =\sqrt{2} \\\\e=\mid AC\mid=\sqrt{ [2-(-3)]^{2} +[2-(-3)]^{2} } =\sqrt{25+25} =\sqrt{50} =\sqrt{5^{2} \cdot 2} =5\sqrt{2}[/tex]

Obliczamy pole rombu.

[tex]P_{romb} =\dfrac{e\cdot f}{2} \\\\P_{romb} =\dfrac{\sqrt{2} \cdot5\sqrt{2} }{2}\\\\\boxed{P_{romb} =5~[j^{2}]}[/tex]