2. Przyporządkuj postacie do odpowiednich opisów: Mahatma Gandhi, Mao Tse-Tung, Nikita Chruszczow, Kim Ir Sen, Fidel Castro, Ho Chi Minh,

a) postać ubrana w czerwone ubranie to Jan Zamoyski - kanclerz i hetman wielki koronny Rzeczpospolitej Obojga Narodów, a postać siedząca z mieczem w ręku to Stefan Batory - król Polski w latach 1576 - 1586.

b) Obraz przedstawiony na ilustracji to "Batory pod Pskowem" Jana Matejki

Odpowiedź:

Odpowiedź w załączniku  liczę na naj :)))

Wyjaśnienie:

Odpowiedź:

[tex]a=5\sqrt{5}[/tex], [tex]P=75[/tex], [tex]|DB|=5\sqrt{2}, |AC|=15\sqrt{2}[/tex]

Szczegółowe wyjaśnienie:

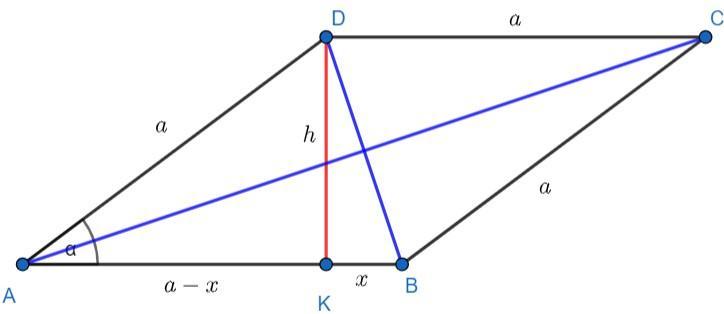
Przyjmijmy oznaczenia takie, jakie są w załączniku.

Pole rombu możemy wyrazić na dwa sposoby:

[tex]P=a^{2} sin\alpha =ah[/tex]

[tex]sin\alpha =\frac{h}{a}[/tex]

Z jedynki trygonometrycznej obliczamy wartość sinusa kąta [tex]\alpha[/tex]:

[tex]cos\alpha =\frac{4}{5}[/tex] ⇒ [tex]sin\alpha =\frac{3}{5}[/tex]

Teraz wstawiamy tę wartość do powyższej zależności i dostajemy:

[tex]\frac{3}{5} =\frac{h}{a}[/tex] ⇒ [tex]3a=5h[/tex]

Wiemy ponadto, że [tex]a+h=8\sqrt{5}[/tex] ⇔ [tex]h=8\sqrt{5} -a[/tex], wstawiamy tę wartość do wcześniejszego równania:

[tex]3a=5(8\sqrt{5} -a)[/tex] ⇔ [tex]3a=40\sqrt{5} -5a[/tex] ⇔ [tex]8a=40\sqrt{5}[/tex] ⇔ [tex]a=5\sqrt{5}[/tex]

Dalej obliczamy wysokość rombu:

[tex]h=8\sqrt{5} -a=3\sqrt{5}[/tex]

Popatrzmy teraz na trójkąt prostokątny [tex]AKD[/tex], z definicji funkcji cosinus obliczamy długość odcinka [tex]x[/tex]:

[tex]cos\alpha =\frac{a-x}{a} =\frac{4}{5}[/tex] ⇔ [tex]5x=a[/tex] ⇔ [tex]x=\frac{5\sqrt{5} }{5} =\sqrt{5}[/tex]

Z twierdzenia Pitagorasa w trójkącie prostokątnym [tex]DKB[/tex] dostaniemy:

[tex]|DB|^{2} =h^{2} +x^{2} =(3\sqrt{5}) ^{2} +(\sqrt{5} )^{2} =50\\|DB|=\sqrt{50} =5\sqrt{2}[/tex]

Obliczamy pole rombu z wcześniejszego wzoru:

[tex]P=75[/tex]

Ze wzoru na pole rombu z przekątnymi obliczamy długość odcinka [tex]|AC|[/tex] :

[tex]P=\frac{1}{2} |DB| |AC|=75[/tex]

[tex]|AC|=15\sqrt{2}[/tex]

Odpowiedź:

2 Is he sending

Yes, he is

3 Are they phoning

No, they aren't

4 Are you reading

Yes, I am

5 Are we listening

No, we aren't

6 Am I going (?)

Yes, I am