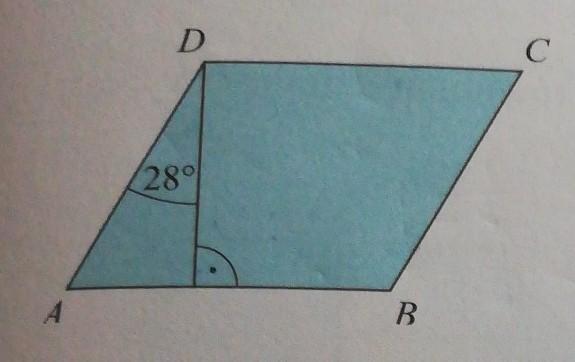
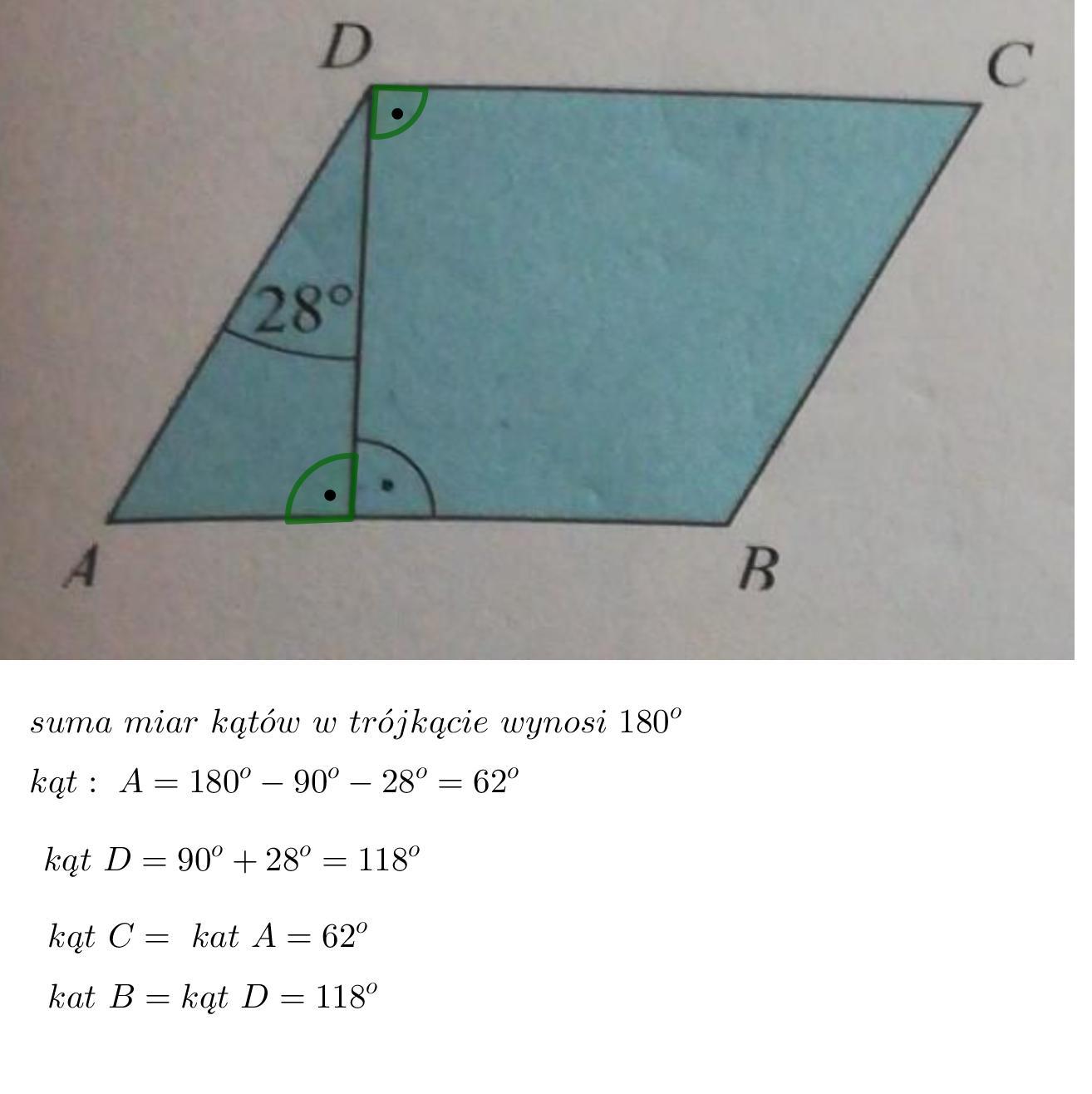
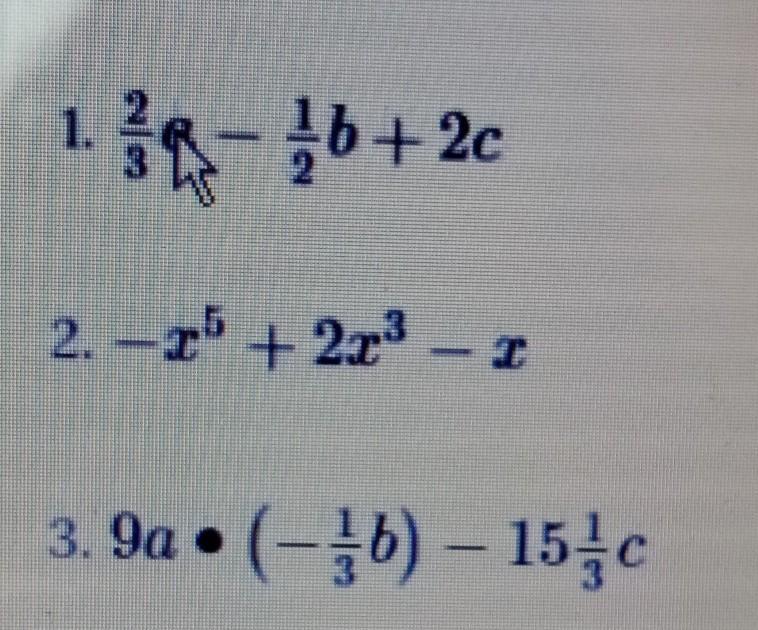wydzielony fragment tekstu zaczynajacy sie od nowego wiersza to?

Temat:
Informatyka
Autor:
allie11
Utworzono:
1 rok temu

Odpowiedzi 1

Wydzielony fragment tekstu zaczynający się od nowego wiersza to akapit.

Autor:

buster7nlq
Oceń odpowiedź:
19

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Proszę o wykonanie zadań z góry dziękuję. 1. Wymień jakie nowe „państwa” powstały na ziemiach polskich po kongresie wiedeńskim. Z jakimi krajami były one związane? 2. Podaj datę wybuchu, przyczyny i skutki powstania listopadowego (należy też wskazać, jakie konkretnie represje dotknęły Królestwo Polskie). 3. Kim byli: Piotr Wysocki, Mikołaj I, Adam Jerzy Czartoryski, Jakub Szela 4. Podaj nazwy czterech stronnictw politycznych Wielkiej Emigracji. Opisz założenia jednego z nich. 5. Wyjaśnij czym była Wielka Emigracja; na czym polegała działalność emisariuszy? 6. Kiedy wybuchło powstanie krakowskie? (rok). Jakie były jego przyczyny i skutki? 7. Wyjaśnij czym charakteryzowały się: romantyzm i mesjanizm.