Rozwiąż zagadkę i odgadnij wyraz

Odpowiedź:

Rozwiązanie w załączniku:

Wyjaśnienie:

j - jedności

d - dziesiątki

s - setki

jt - jedności tysięcy

dt - dziesiątki tysięcy

st - setki tysięcy

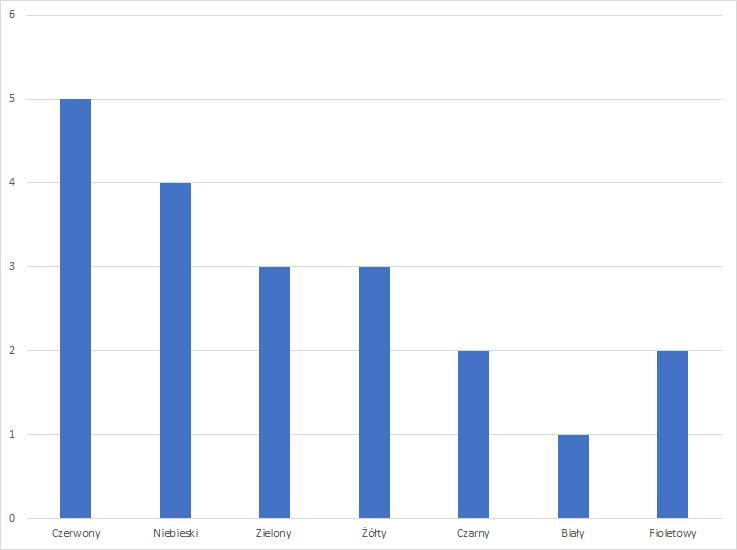
Zadanie jest do własnego wykonania. Tutaj natomiast mogę pokazać na przykładzie jak należy opracować otrzymane dane.

Załóżmy, że wśród 20-osobowej grupy mamy następujące ulubione kolory:

• czerwony - 5 osób,
• niebieski - 4 osoby,
• zielony - 3 osoby,
• żółty - 3 osoby,
• czarny - 2 osoby,
• biały - 1 osoba,
• fioletowy - 2 osoby.

Dla powyższych danych możemy stworzyć diagram słupkowy:

1. na poziomej osi zapisujemy ulubiony kolor,
2. na pionowej osi liczbę osób, która lubi dany kolor,
3. rysujemy nad każdym z kolorów odpowiednio długi słupek.

Diagram słupkowy dla powyższych danych przedstawiono w załączniku.

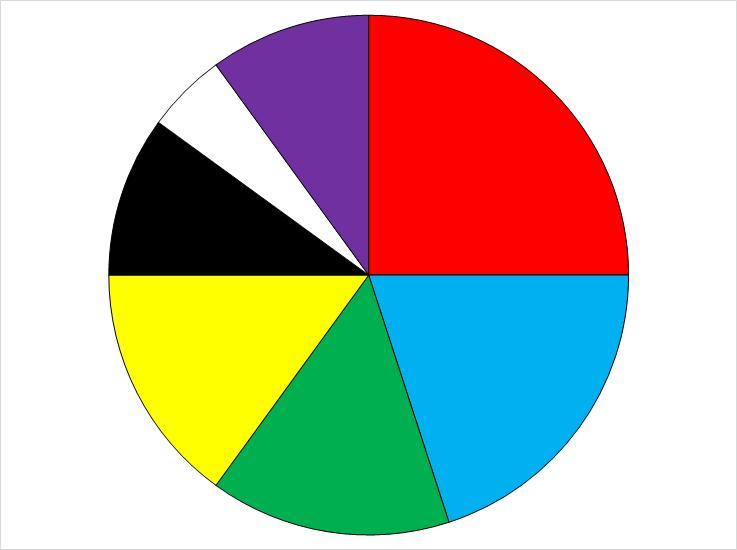
Aby narysować diagram kołowy najpierw musimy obliczyć jaką część grupy stanowią osoby lubiące dany kolor, a następnie obliczyć ile to będzie stopni w kole.

Czerwony:

[tex]\frac{5}{20}=\frac{1}{4}[/tex]

[tex]\frac{1}{4}\cdot360^\circ=90^\circ[/tex]

Niebieski:

[tex]\frac{4}{20}=\frac{1}{5}[/tex]

[tex]\frac{1}{5}\cdot360^\circ=72^\circ[/tex]

Zielony:

[tex]\frac{3}{20}[/tex]

[tex]\frac{3}{20}\cdot360^\circ=54^\circ[/tex]

Żółty:

[tex]\frac{3}{20}[/tex]

[tex]\frac{3}{20}\cdot360^\circ=54^\circ[/tex]

Czarny:

[tex]\frac{2}{20}=\frac{1}{10}[/tex]

[tex]\frac{1}{10}\cdot360^\circ=36^\circ[/tex]

Biały:

[tex]\frac{1}{20}[/tex]

[tex]\frac{1}{20}\cdot360^\circ=18^\circ[/tex]

Fioletowy:

[tex]\frac{2}{20}=\frac{1}{10}[/tex]

[tex]\frac{1}{10}\cdot360^\circ=36^\circ[/tex]

Mając obliczone, jakie kąty mają zająć poszczególne kolory, możemy narysować diagram kołowy (rysunek w załączniku).

Odpowiedź:

B partykułą , 2 wyrazić przypuszczenie

Odpowiedź: b) partykuła

Wyjaśnienie:

2)

wyrażająca przypuszczenie mówiącego, że komunikowany w zdaniu sąd jest prawdziwy, np. Chyba doszliśmy do porozumienia.»