Strona bierna (czasowniki modalne). Uzupełnij zdania używając strony biernej. Daje naj!
-
Temat:
Język angielski -
Autor:
maggie -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
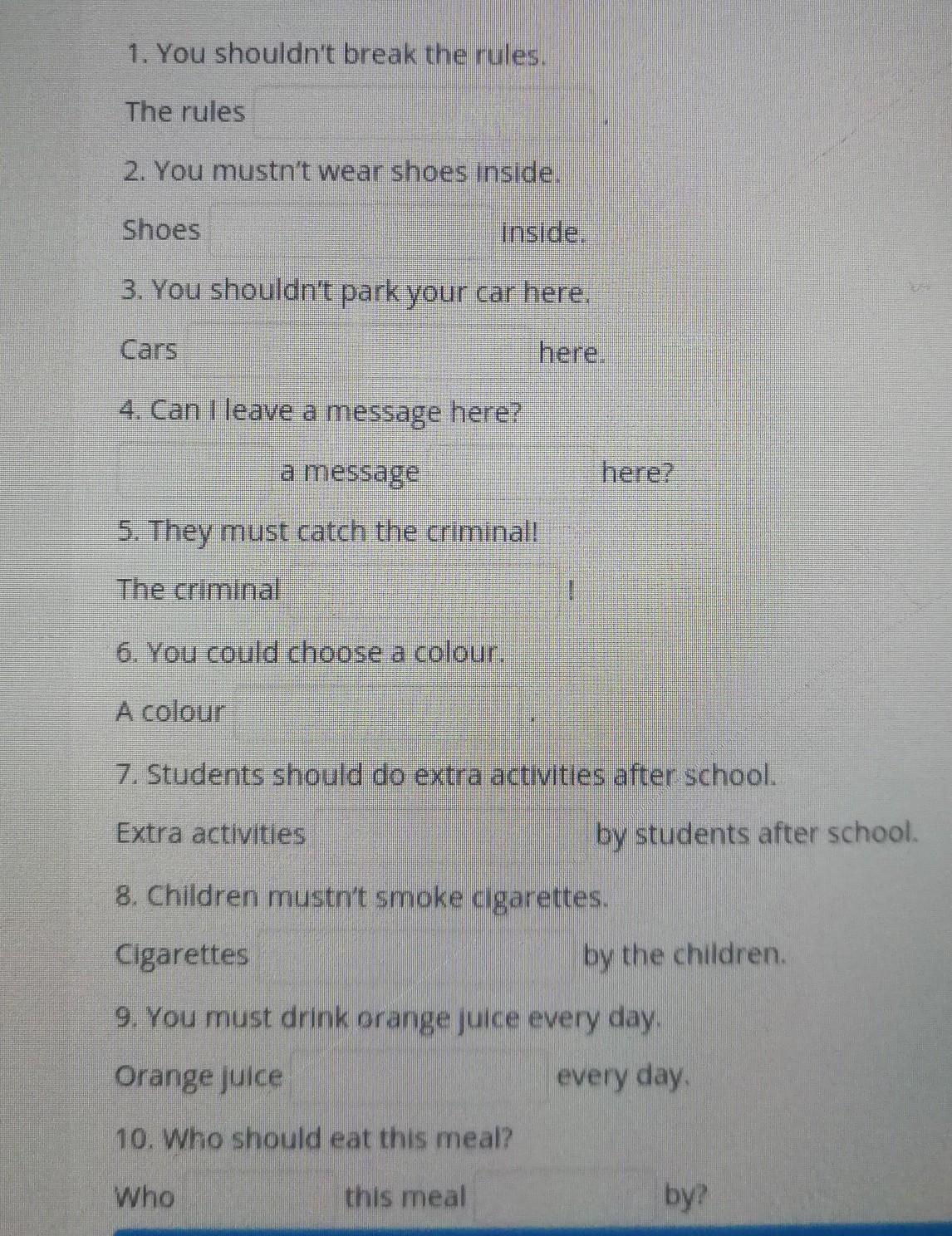
1 shouldn't be broken
2 mustn't be worn
3 shouldn't be parked
4 Can … be left
5 must be caught
6 could be chosen
7 should be done
8 mustn't be smoked
9 must be drunk
10 should … be eaten
-
Autor:
rafaelaooh
-
Oceń odpowiedź:
7
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years




