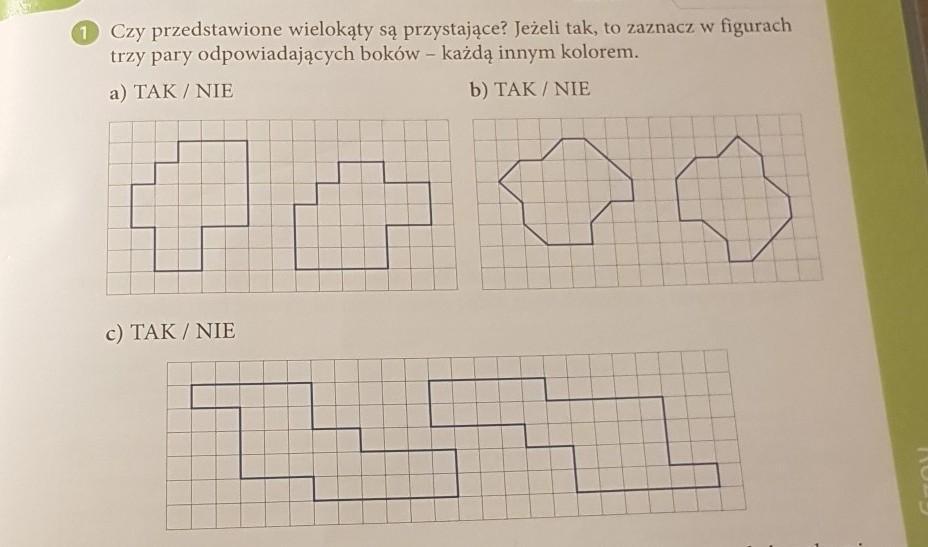
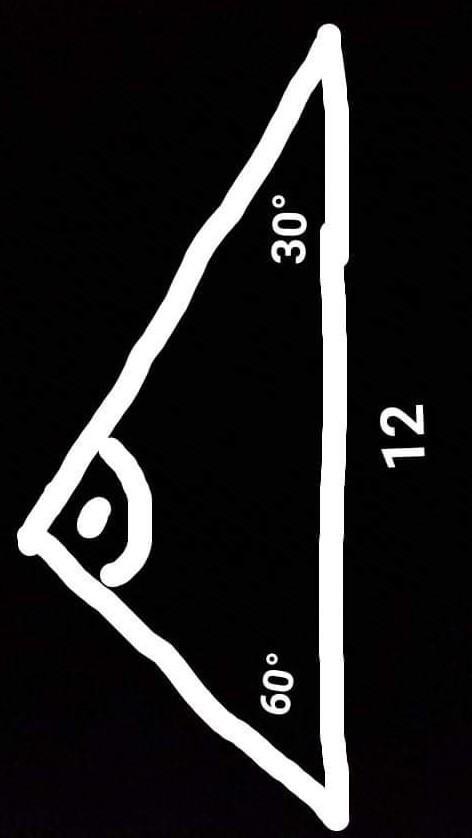
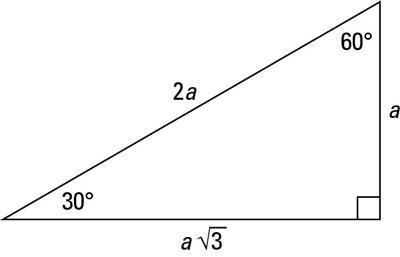
Completa con las formas adecuadas del verbo estudiar. Uzupełnij właściwymi formami czasownika estudiar. 1. Yo 2. Tú 3. Él, ella, usted 4. Nosotros/as 5. Vosotros/as 6. Ellos, ellas, ustedes
-
Temat:
Język hiszpański -
Autor:
huang -
Utworzono:
1 rok temu
Odpowiedzi 1
Yo Estudio
Tu Estudias
El/Ella/Usted Estudia
Nosotros Estudiamos
Vosotros Estudiais
Ellos/Ellas/Ustedes Estudian
-
Autor:
butchdaniels
-
Oceń odpowiedź:
5
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
everett57
-
Autor:
peanutl5a8
-
Oceń odpowiedź:
15
-
Autor:
drew38
-
Autor:
sebastiánreese
-
Oceń odpowiedź:
15
-
Autor:
adrianna
Odpowiedź:
[tex]\huge\boxed{P=18\sqrt3}[/tex]
Szczegółowe wyjaśnienie:
Możemy rozwiązać to zadanie na dwa sposoby:
SPOSÓB 1:Patrz załącznik.
Z rysunku mamy dane:
[tex]2a=12[/tex]
stąd
[tex]a=12:2=6\\\\a\sqrt3=6\sqrt3[/tex]
Pole trójkąta prostokątnego o przyprostokątnych a i b:
[tex]P=\dfrac{a\cdot b}{2}[/tex]
Podstawiamy długości przyprostokątnych:
[tex]P=\dfrac{6\cdot6\sqrt3}{2}=18\sqrt3[/tex]
SPOSÓB 2:Trójkąt ten stanowi połowę trójkąta równobocznego o boku długości równej długości przeciwprostokątnej.
Wzór na pole trójkąta równobocznego o boku a:
[tex]P=\dfrac{a^2\sqrt3}{4}[/tex]
Czyli pole naszego trójkąta to:
[tex]P=\dfrac{1}{2}\cdot\dfrac{12^2\sqrt3}{4}=\dfrac{144\sqrt3}{8}=18\sqrt3[/tex]
-
Autor:
laylahcuevas
-
Oceń odpowiedź:
8