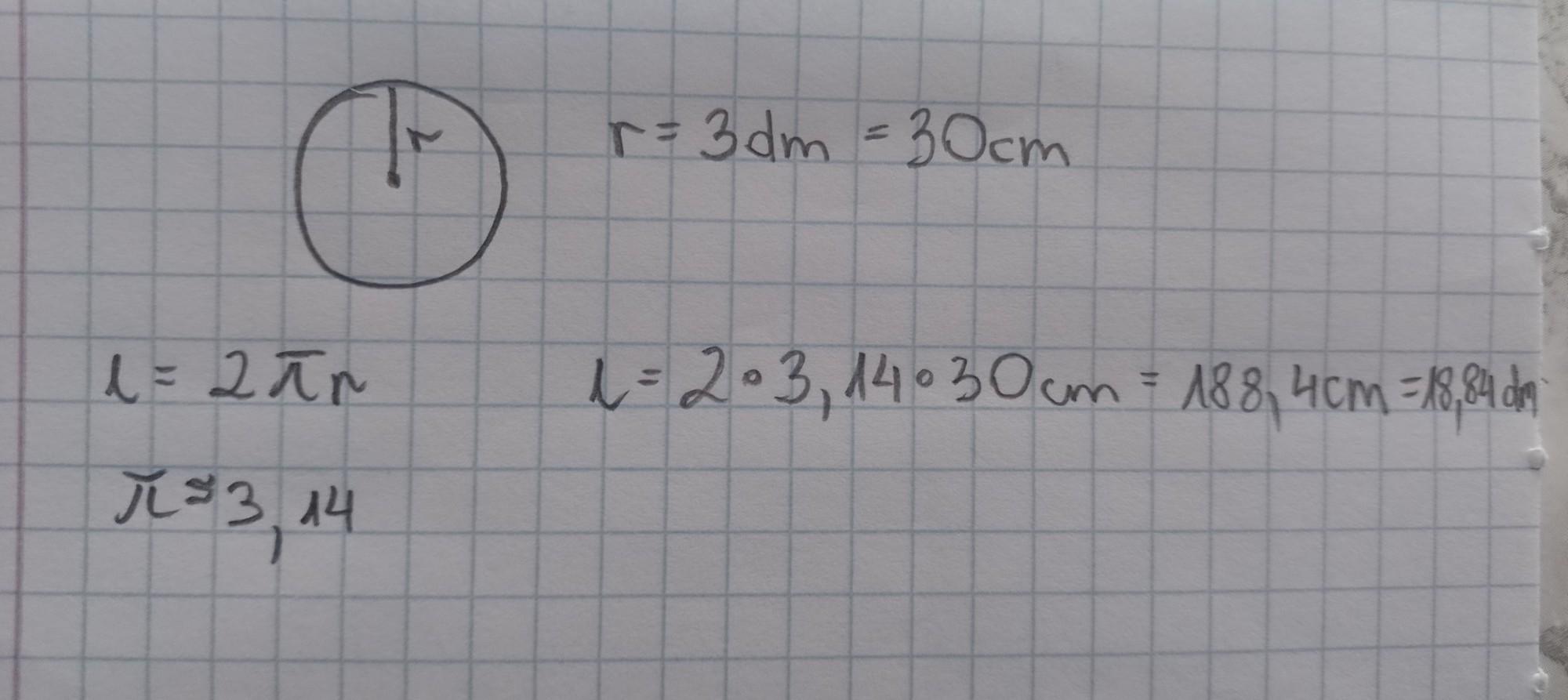opisz wyjazd do Berlina po niemieckuwyjazd skąd, o której, jakim transportem ewentualna przesiadka np w samolotprzyjazd o którejkoszt całej podróżyto samo z drogą powrotną​

Odpowiedzi 1

Wyjaśnienie:

aus Polen um 10 Uhr mit dem Auto, Umsteigen in ein Flugzeug um 20 Uhr, Kosten 100 PLN

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Oblicz przybliżoną długość okręgu, którego promień jest równy 3 dm. Wynik podaj z dokładnością do dziesiątych części decymetra. Przyjmij ~ 3, 14.poproszę jeszcze dziś​

Odpowiedź:

L ≈ 188,4 cm

Szczegółowe wyjaśnienie:

[tex]r = 3 \ dm = 3 0 \ cm\\\pi\approx3,14\\L = ?[/tex]

Korzystamy ze wzoru na długość okręgu:

[tex]L = 2\pi r\\\\L \approx2\cdot3,14\cdot30 \ cm\\\\\boxed{L\approx 188,4 \ cm}[/tex]

Odpowiedź:

Długość okręgu wynosi dokładnie 188,4cm czyli 18,84dm. W przybliżeniu 190cm lub 19dm

answer img
napisz list motywacyjny do szkoły do której chcesz się dostać
Szanowny dyrektorze( czy do kogo tam piszesz)Z wielka przyjemnością aplikuje o miejsce w waszej szkole.Uważam, ze wasza społeczność reprezentuje sobą wartości, które dla mnie są istotne i pragnę stać się jej częścią. Myśle ze mogłabym wnieść wiele korzystnych zmian i przyłożyć się do wspólnego celu jakim jest by była ona otwarta i przyjazna wszystkim.Dlaczego uważam, że nadaje sie na ucznia waszej szkoły?-Ukończyłam podstawówkę z zachowaniem wzorowym, gdyż zawsze jestem chętna do pomocy uczniom i nauczycielom oraz zachowuje sie nienagannie i z grzecznością odnoszę sie do wszystkich.-Świadectwo otrzymałam z czerwonym paskiem, ponieważ przedkładam wiedzę nad wszystkie inne wartości oraz zależy mi na mojej przyszłości.-Uczęszczalam na wolontariat i kółka zainteresowań, co świadczy o moim zaangażowaniu w życie społeczne.-Uczestniczyłam w wielu konkursach jak między innymi …. co pokazuje moja determinację do nauki.-Posiadam wiele pozaszkolnych zainteresowań jak np. gra na gitarze czy gra w siatkówkę.Przede wszystkim myślę, że nadaje sie na ucznia waszej szkoły gdyż jestem w stanie uczynić ją lepszym miejscem dla każdego z nas.Mam nadzieje, że będę mogła zobaczyć sie z panem osobiście już jako uczennica tej szkoły.Z wyrazami szacunku XYZ
Oblicz długość przekątnej prostopadłościanu o krawędziach 9cm,6cm i 2 cm.

Odpowiedź:

p² = 9² + 6² + 2² = 81 + 36 + 4 = 121

p = [tex]\sqrt{121}[/tex] = 11

p = 11 cm

=========

Szczegółowe wyjaśnienie:

Bardzo proszę szybko
question img

[tex]Dane:\\m = 46 \ kg\\M_{p} = 2,4M_{z}\\R_{p} = 1,4R_{z}\\g_{z} = 10\frac{m}{s^{2}}\\Szukane:\\Q_{p} = ? \ - \ ciezar \ na \ planecie[/tex]

Rozwiązanie

Ciężar ciała zależy od masy ciała (która jest wartością stałą) oraz od wartości przyspieszenia grawitacyjnego:

[tex]Q = m\cdot g[/tex]

[tex]gdzie:\\g = \frac{M}{R^{2}}[/tex]

[tex]g_{z} = \frac{GM_{z}}{R_{z}^{2}}[/tex]

[tex]g_{p} = \frac{G\cdot2,4M_{z}}{(1,4R_{z})^{2}} = \frac{2,4GM_{z}}{1,96R_{z}^{2}} = \frac{2,4}{1,96}g_{z}=\frac{2,4}{1,96}\cdot10\frac{m}{s^{2}}\\\\Q_{p} = m\cdot g_{p}\\\\Q_{p} = 46 \ kg\cdot\frac{2,4}{1,96}\cdot10\frac{m}{s^{2}}\\\\\boxed{Q_{p} = 563,27 \ N}\\\\\underline{Odp. \ c)}[/tex]

Other Język niemiecki Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years