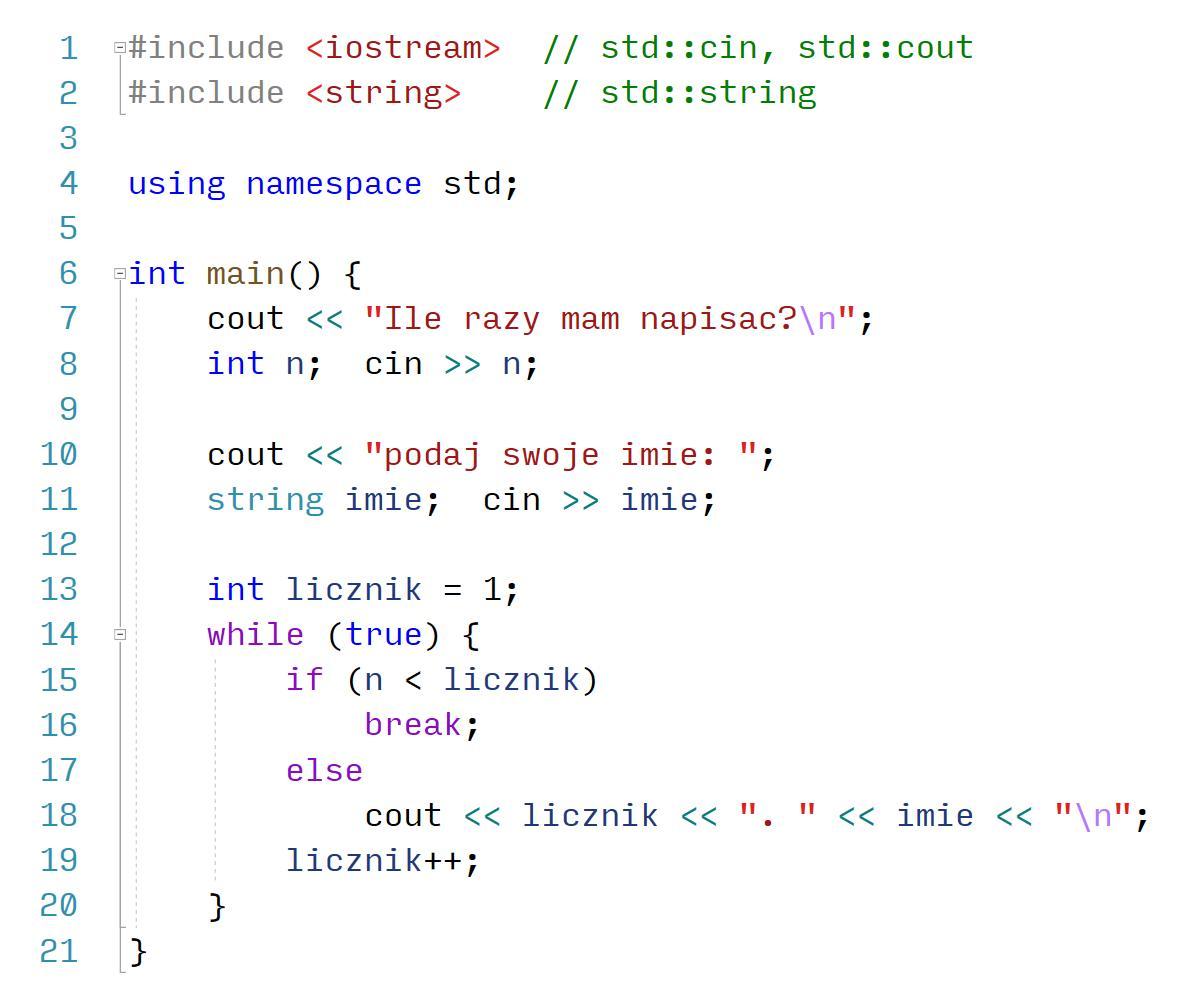
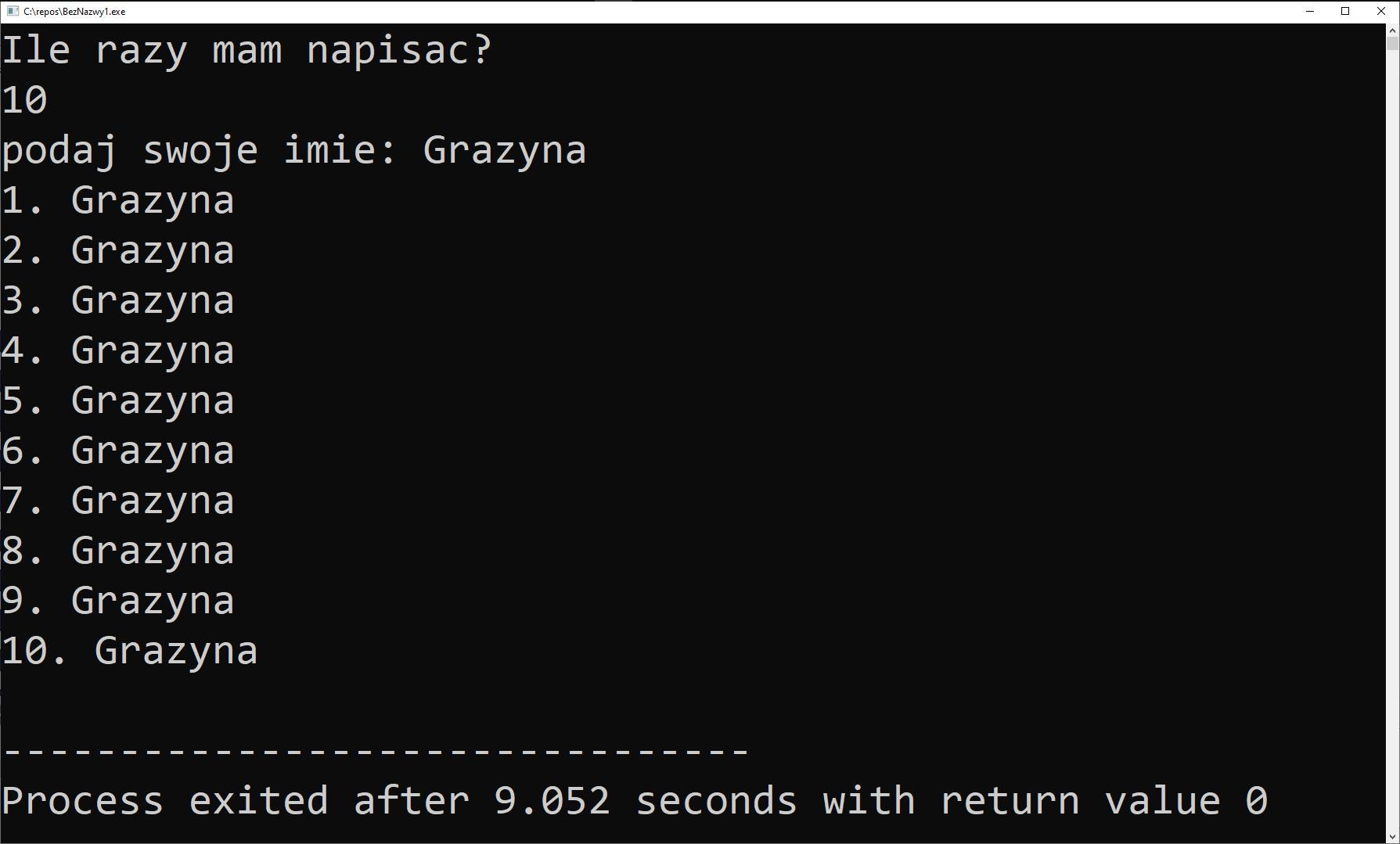
Ich heisse Nikodem. Ich bin 12 Jahre alt. Ich wohne in Wrocław. Und ich komme aus Polen. Jeden Tag stehe ich um halb sechs Uhr auf. Ich esse mein Frühstück um sieben Uhr. Ich fahre zur Schule um halb acht Uhr. Ich fahre um fünfzehn Uhr zurück. Ich esse zu Mittag um achtzehn Uhr. Ich mache die Hausaufgaben und ich sehe fern. Mein Hobby ist Tennis. Ich kann sehr gut Tennis spielen und schwimmen Ich kann nicht sehr gut surfen und ich muss einen Surfkurs besuchen. Ich will einen Reitkurs besuchen. PYTANIA DO WSZYSTKIEGO !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Ta teza jest dobra.

Odpowiedź:

7√2*3√3=7*3*√(2*3)=21√6

3∛3*4∛7=3*4*∛(3*7)=12∛21

4∛(-6)/2∛(-2)=2∛3

√3,5:2√(7/8)=√(3,5: 0,875) /2= √4/2=2/2=1

3√5*√6/2√2=3√30/2√2= 3√15/2=1,5√15

∛(1/3) *2∛6=2*∛(1/3*6)=2∛2

1-   3√5/√125=  1-   3√5 /√(25*5)=1 -  3√5/5√5= 1-3/5=2/5

√0,8:√0,008/(-0,1)²= √(0,8:0,008) *100=√100   *100=10*100=1000

Szczegółowe wyjaśnienie:

Szczegółowe wyjaśnienie:

Na kostce mamy 6 różnych wyników. Stąd mamy

6 · 6 · 6 · 6 · 6 · 6 · 6 · 6 · 6 = 6⁹

Teraz mamy obliczyć ile różnych wyników otrzymamy takich, że w pierwszym, trzecim i ósmym rzucie wypadnie ten sam wynik.

W treści zadania nie ma, że tylko w tych rzutach ma być ten sam wynik.

Stąd:

1 · 6 · 1 · 6 · 6 · 6 · 6 · 1 · 6 = 6⁶ tyle wyników z jedną z sześciu możliwości

czyli wszystkich

Jeżeli na innych kostkach ma być inna liczba oczek, wówczas mamy:

1 · 5 · 1 · 5 · 5 · 5 · 5 · 1 · 5 = 5⁶ tyle wyników z jedną z sześciu możliwości

czyli wszystkich

Potrzebne wzory:

Pole podstawy stożka:

r - promień koła w podstawie

Pole powierzchni bocznej stożka:

r - promień koła w podstawie

l - tworząca

Mamy daną wysokość stożka H = 8 i tworzącą l = 9.

Brakuje nam długości promienia koła w podstawie.

Obliczymy ją stosując twierdzenie Pitagorasa (patrz załącznik).

a,b - długości przyprostokątnych

c - długość przeciwprostokątnej

Podstawiamy:

r² + 8² = 9²

r² + 64 = 81     |-64

r² = 17

Obliczamy pola:

Pp = π · (√17)²

Pb = π · √17 · 9

Stosunek pola powierzchni bocznej stożka do pola podstawy stożka:

Pb/Pp = (9π√17)/(17π)

Odpowiedź:

#include <iostream>

using namespace std;

int main() {

 int n,i;

 string imie;

 cout<<"Ile razy mam powtórzyć?: ";

 cin>>n;

 cout<<"Podaj imię: ";

 cin>>imie;

 for (i=1;i<=n;i++)

   cout<<i<<". "<<imie<<endl;

}

Wyjaśnienie:

Odpowiedź:

To jest zadanie szkolne i jako takie należy je zrobić pętlą  while  oraz właśnie przy pomocy  if  oraz  break.

Przykładowy kod źródłowy dałam w pierwszym załączniku.W drugim załączniku pokazałam przykładowe wyniki uruchomienia kodu źródłowego przy użyciu programu Dev-C++. Wybrałam Dev-C++ ponieważ przykład w zadaniu pochodzi z tego właśnie programu.  ( Czas wykonania zależy głównie od tego jak szybko się pisze. :-)  )

Wyjaśnienie

W latach 60-tych i 70-tych gdy pisano (w Polsce) programy szkolne – przesadziłam, :-) na uczelniach wyższych – w językach Algol i FORTRAN byłaby to pętla z użyciem goto oraz if (GOTO i IF). Ale pod koniec lat 70-tych zaczęto uczyć przy użyciu języka Pascal i w językach wysokiego poziomu goto stało się rzadko używaną ciekawostką.