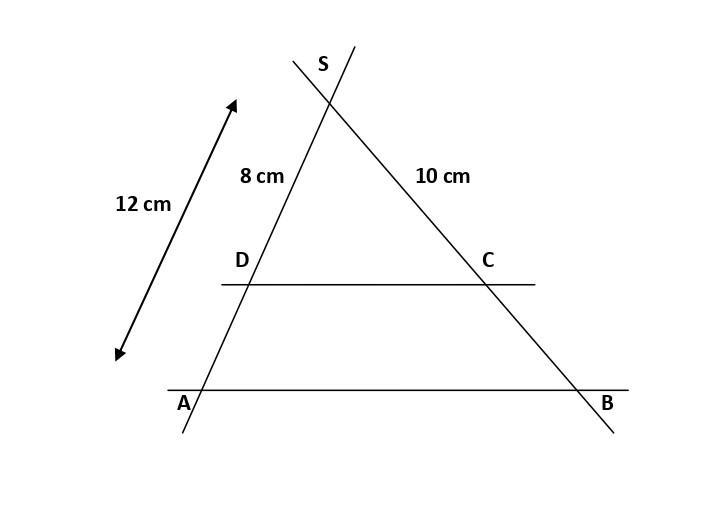
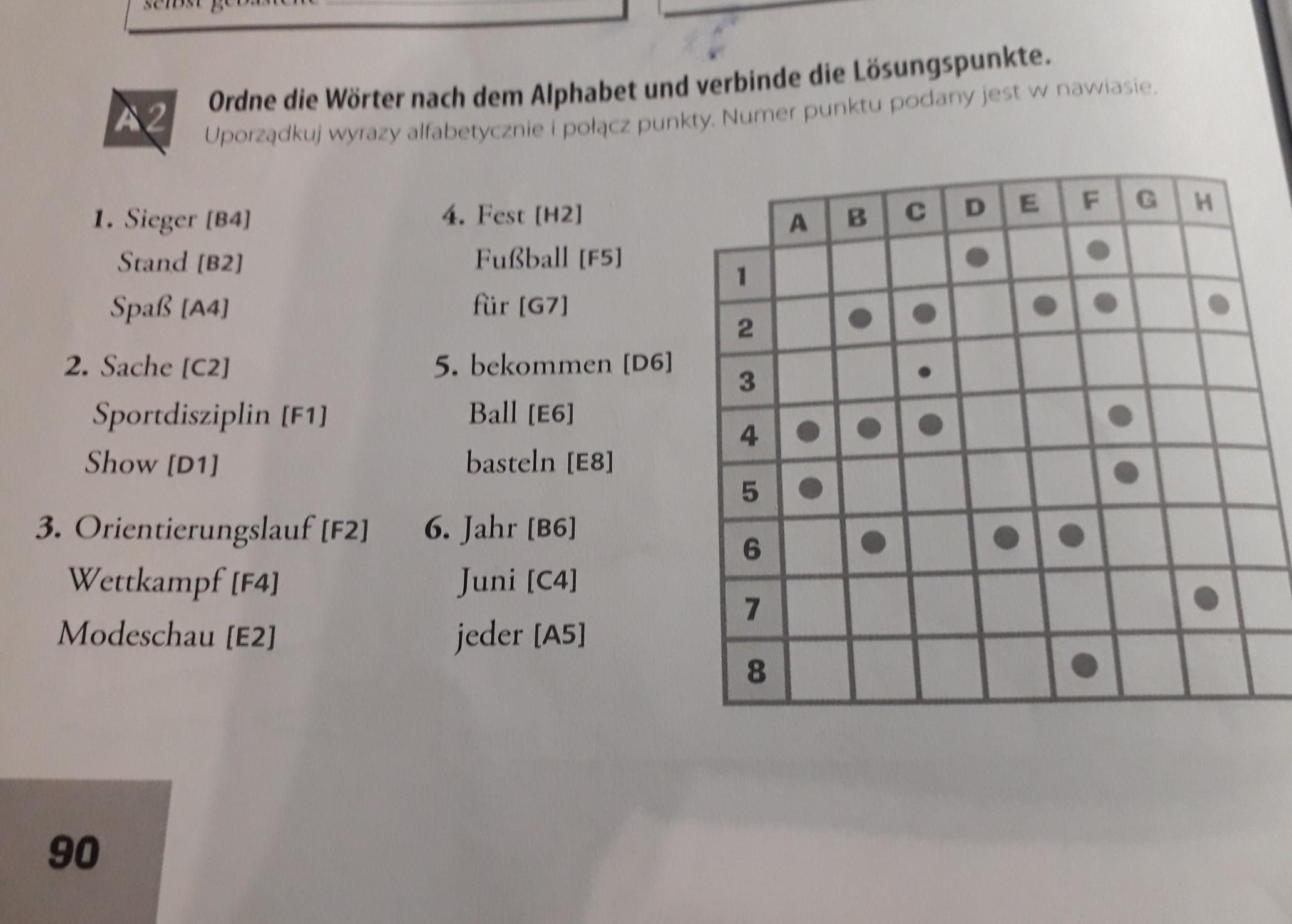
A2 Ordne die Wörter nach dem Alphabet und verbinde die Lösungspunkte. Uporządkuj wyrazy alfabetycznie i połącz punkty. Numer punktu podany jest w nawiase 1. Sieger [B4] 4. Fest [H2] F G и A B DE C Stand [B2] Spaß [A4] 2. Sache [C2] ● Sportdisziplin [F1] Show [D1] 3. Orientierungslauf [F2] Wettkampf [F4] Modeschau [E2] Fußball [F5] für [G7] 5. bekommen [D6] Ball [E6] basteln [E8] 6. Jahr [B6] Juni [C4] jeder [A5] 1 2 3 4 5 6 7 8 ● DO ● ● PROSZEEE
-
Temat:
Język niemiecki -
Autor:
boomer -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
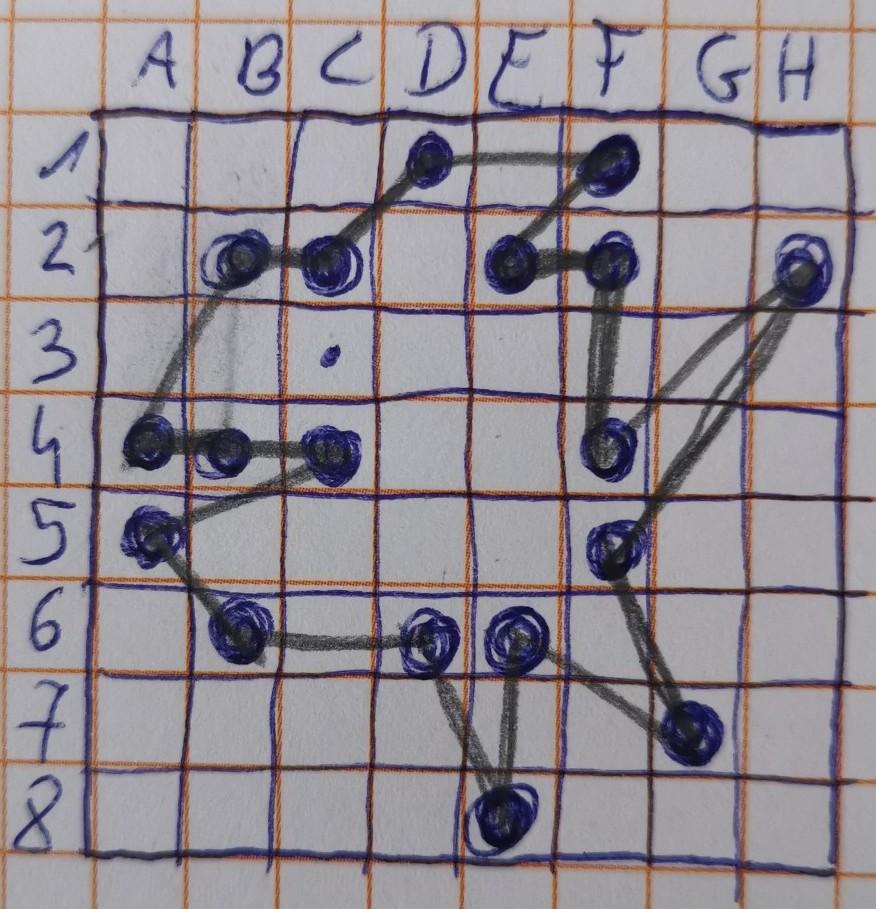
W załączniku znajduje się połączenie punktów :)
-
Autor:
aylinegji
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
graysontran
-
Autor:
ticklesv0mi
-
Oceń odpowiedź:
10
-
Autor:
leyla
-
Autor:
frodorodgers
-
Oceń odpowiedź:
9
-
Autor:
raymacias
Ramię BC trapezu ABCD ma długość [tex]5 cm[/tex].
Skąd to wiadomo?
Sytuację opisaną w zadaniu przelano na "papier". Odpowiedni rysunek wraz z oznaczeniami znajduje się w załączniku.
Z treści zadania wiadomo, że:
- odcinek AS ma długość [tex]12 cm[/tex],
- odcinek CS ma długość [tex]10 cm[/tex],
- odcinek DS ma długość [tex]8 cm[/tex].
Krok 1
Dysponując powyższymi informacjami jesteśmy w stanie obliczyć długość odcinka AD:
[tex]12 - 8 = 4(cm)[/tex]
Krok 2
Teraz można wykorzystać twierdzenie Talesa. O czym ono mówi? Mamy pewien kąt (w naszym przypadku ∡ ASB). Przecinają go dwie proste równoległe względem siebie (w naszym przypadku to proste zawierające odcinki CD i AB - podstawy w trapezie są równoległe). Podzieliły one ramiona kąta na odcinki. Stosunki odpowiednich odcinków są równe. Możemy dzięki temu zapisać:
[tex]\frac{|DS|}{|CS|} =\frac{|AD|}{|BC|} \\\frac{8}{10} =\frac{4}{|BC|} \\8*|BC|=4*10\\8*|BC|=40\\|BC|=5(cm)[/tex]
W ten sposób poznaliśmy długość ramienia BC trapezu.
#SPJ1
-
Autor:
raúlhardy
-
Oceń odpowiedź:
8
