Krzyżówka Sportowa. Pomocy NA TERAZ

Odpowiedź:

zad.1

Na mocy tych ustaw, ludność zydowska została pozbawiona większości praw obywatelskich. Prawo do niemieckiego obywatelstwa, miały tylko osoby posiadające "niemiecką krew". W związku z tym, żydów wykluczono całkowicie z niemieckiego życia państwowego, kulturalnego i publicznego (nie mogli np. korzystać ze środków transportu czy wchodzić do restauracji). Dodatkowo wprowadzono zakaz zawierania mieszanych małżeństw i segregację rasową w Niemczech.

Zad. 2.

Naziści pozbawili Żydów prawa noszenia niemieckich symboli narodowych- miało to na celu wykluczenie ich ze społeczeństwa (aby nie czuli się ich częścią). Ludność żydowska nie mogła podnosić flagi państwowej na uroczystościach. Mogli jedynie identyfikować się z żydowskimi kolorami i emblematami

Wyjaśnienie:

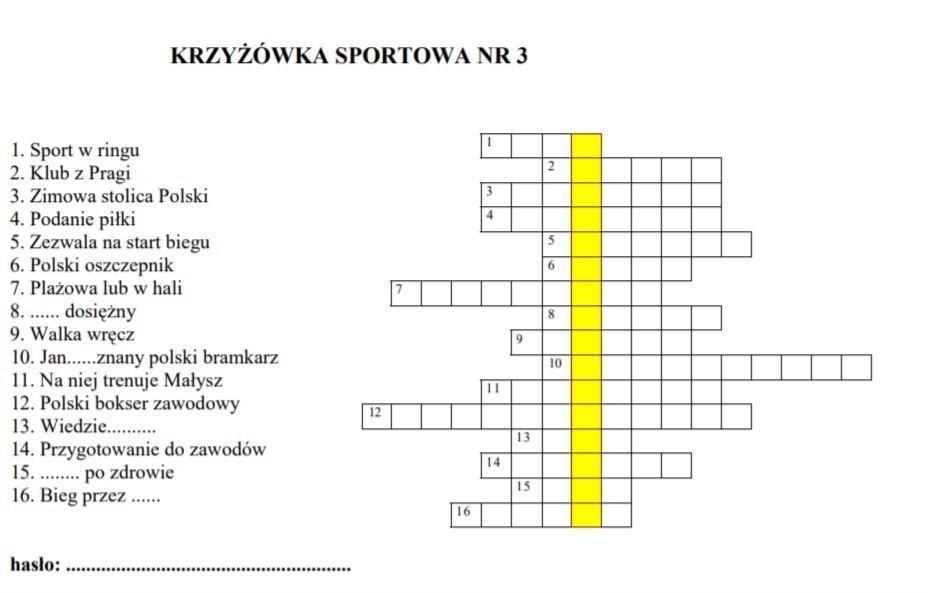
W zadaniu należy wykonać obliczenia według wzoru.

Pamiętajmy, że:

[tex]\sqrt{a^2} = a \\\\\sqrt[3]{a^3} = a \\\\[/tex]

oraz:

[tex]\sqrt[3]{a^6} = \sqrt[3]{(a^2)^3} = a^2 \\\\\sqrt[3]{a^9} = \sqrt[3]{(a^3)^3} = a^3 \\\[/tex]

Przedstawiamy liczby tak jak w pokazanych przykładach.

[tex]a) \\\\\sqrt{16 \cdot 9} = \sqrt{16} \cdot \sqrt{9} = 4 \cdot 3 = 12 \\\\b) \\\\\sqrt{100 \cdot 64} = \sqrt{100} \cdot \sqrt{64} = 10 \cdot 8 = 80 \\\\c) \\\\\sqrt{6^2 \cdot 5^2} = \sqrt{6^2} \cdot \sqrt{5^2} = 6 \cdot 5 = 30 \\\\d) \\\\\sqrt{4 \cdot 81 \cdot 9} = \sqrt{4} \cdot \sqrt{81} \cdot \sqrt{9} = 2 \cdot 9 \cdot 3 = 54 \\\\[/tex]

[tex]e) \\\\\sqrt{16 \cdot 25 \cdot 49} = \sqrt{16} \cdot \sqrt{25} \cdot \sqrt{49} = 4 \cdot 5 \cdot 7 = 140 \\\\f) \\\\\sqrt{11^2\cdot2^2 \cdot 3^4} = \sqrt{11^2} \cdot \sqrt{2^2} \cdot \sqrt{3^4} = 11 \cdot 2 \cdot 3^2 = 22 \cdot 9 =198\\\\g) \\\\\sqrt[3]{27 \cdot 64} = \sqrt[3]{27} \cdot \sqrt[3]{64} = 3 \cdot 4 = 12\\\\h) \\\\\sqrt[3]{8 \cdot 64} = \sqrt[3]{8} \cdot \sqrt[3]{64} = 2 \cdot 4 = 8\\\\[/tex]

[tex]i) \\\\\sqrt[3]{7^3 \cdot 9^3} = \sqrt[3]{7^3} \cdot \sqrt[3]{9^3} = 7 \cdot 9 = 63\\\\j) \\\\\sqrt[3]{27 \cdot 64 \cdot 125} = \sqrt[3]{27} \cdot \sqrt[3]{64} \cdot \sqrt[3]{125} = 3 \cdot 4 \cdot 5 = 60\\\\k) \\\\\sqrt[3]{3^6 \cdot 5^3 \cdot 2^9} = \sqrt[3]{3^6} \cdot \sqrt[3]{5^3} \cdot \sqrt[3]{2^9} = 3^2 \cdot 5 \cdot 2^3 = 9 \cdot 5 \cdot 8 = 360\\\\[/tex]

[tex]l) \\\\\sqrt[3]{4^9 \cdot 6^3 \cdot 2^7} = \sqrt[3]{4^9} \cdot \sqrt[3]{6^3} \cdot \sqrt[3]{27} = 4^3 \cdot 6 \cdot 3 = 64 \cdot 18 = 1152[/tex]

#SPJ2

Stałocieplność, czyli zdolność do utrzymywania stałej temperatury ciała pozwala mu przetrwać w tych skrajnych warunkach, Niedzwiedzie nie są zmiennocieplne, więc ich temperatura ciała nie zmienia się wraz z temperaturą otoczenia.

Miłego dnia

Odpowiedź:

Korony drzew-wiewiórka

Ląd-sarna

gleba-kret

woda-foka

powietrze-nietoperz

licze na naj ❤

Wyjaśnienie: