proszę o szybką odpowiedź !!​

Odpowiedź:

a) jest to trójkąt 3,4,5 znane to poza tym jak cos to Pitagoras a więc tg to a/b to sin to a/c więc

[tex] \sin( \alpha ) = \frac{3}{5} \\ \cos( \alpha ) = \frac{4}{5} [/tex]

b)

[tex] \tan( \alpha ) = \frac{ \sin( \alpha ) }{ \cos( \alpha ) } \\ 3 = \frac{ \sin( \alpha ) }{ \cos( \alpha ) } \\ 3 \cos( \alpha ) = \sin( \alpha ) \\ (3 \cos( \alpha ))^{2} + \cos( \alpha )^{2} = 1 \\ 10 \cos( \alpha ) ^{2} = 1 \\ \sqrt{10} \cos( \alpha ) = 1 \\ \cos( \alpha ) = \frac{ \sqrt{10} }{10} \\ \sin( \alpha ) = \frac{3 \sqrt{10} }{10} \\ lub \\ \cos( \alpha ) = -\frac{ \sqrt{10} }{10} \\ \sin( \alpha ) = - \frac{3 \sqrt{10} }{10} [/tex]

c)

[tex] \tan( \alpha ) = \frac{1}{7} \\ \frac{ \sin( \alpha ) }{ \cos( \alpha ) } = \frac{1}{7} \\ \frac{7 \sin( \alpha ) }{ \cos( \alpha ) } = 1 \\ 7 \sin( \alpha ) = \cos( \alpha ) \\ \sin( \alpha )^{2} + (7 \sin( \alpha )) ^{2} = 1 \\ 50 \sin( \alpha ) ^{2} = 1 \\ \sin( \alpha ) = \frac{ \sqrt{50} }{50} \\ \cos( \alpha ) = \frac{7 \sqrt{50} }{50} \\ lub \\ \sin( \alpha ) = -\frac{ \sqrt{50} }{50} \\ \cos( \alpha ) = -\frac{7 \sqrt{50} }{50} [/tex][/tex]

Odpowiedź:

Szczegółowe wyjaśnienie:

Ćw.5

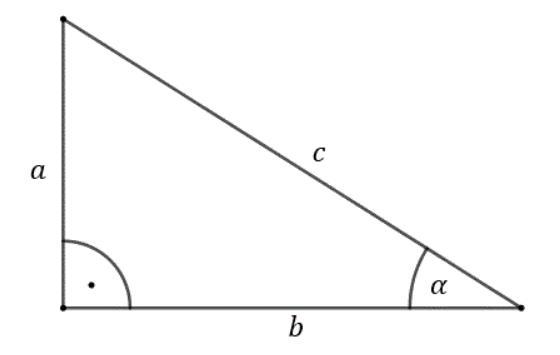
Rysunek w załączniku

sinα= (przyprostokątna leżąca naprzeciwko kąta α) : (przeciwprostokątna) = a:c

cosα= (przyprostokątna leżąca przy kącie α) : (przeciwprostokątna) = b:c

tgα= (przyprostokątna leżąca naprzeciwko kata α) : (przyprostokątna leżąca przy kącie α) = a:b

ctgα= (przyprostokątna leżąca przy kącie α) : (przyprostokątna leżąca naprzeciwko kata α) = b:a

a)

[tex]tg\alpha=\frac{3}{4}=\frac{a}{b}\\a=3\\b=4[/tex]

Wyliczmy c z twierdzenia Pitagorasa

[tex]3^2+4^2=c^2\\9+16=c^2\\c^2=25\\c=\sqrt{25}=5[/tex]

[tex]sin\alpha=\frac{a}{c}=\frac{3}{5}\\\\cos\alpha=\frac{b}{c}=\frac{4}{5}[/tex]

b)

[tex]tg\alpha=3=\frac{3}{1}=\frac{a}{b}\\a=3\\b=1[/tex]

Wyliczmy c z twierdzenia Pitagorasa

[tex]3^2+1^2=c^2\\9+1=c^2\\c^2=10\\c=\sqrt{10}[/tex]

[tex]sin\alpha=\frac{a}{c}=\frac{3}{\sqrt{10}}*\frac{\sqrt{10}}{\sqrt{10}}=\frac{3\sqrt{10}}{10}\\\\cos\alpha=\frac{b}{c}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{\sqrt{10}}=\frac{\sqrt{10}}{10}[/tex]

c)

[tex]tg\alpha=\sqrt{15}=\frac{\sqrt{15}}{1}=\frac{a}{b}\\a=\sqrt{15}\\b=1[/tex]

Wyliczmy c z twierdzenia Pitagorasa

[tex](\sqrt{15})^2+1^2=c^2\\15+1=c^2\\c^2=16\\c=\sqrt{16}=4[/tex]

[tex]sin\alpha=\frac{a}{c}=\frac{\sqrt{15}}{4}\\\\cos\alpha=\frac{b}{c}=\frac{1}{4}[/tex]

Zad.1.

a)

[tex]sin\alpha=0,8=\frac{4}{5}=\frac{a}{c}\\a=4\\c=5[/tex]

Wyliczmy b z twierdzenia Pitagorasa

[tex]4^2+b^2=5^2\\16+b^2=25//-16\\b^2=9\\b=\sqrt{9}=3[/tex]

[tex]cos\alpha=\frac{b}{c}=\frac{3}{5}\\\\tg\alpha=\frac{a}{b}=\frac{4}{3}=1\frac{1}{3}\\\\ctg\alpha=\frac{b}{a}=\frac{3}{4}[/tex]

b)

[tex]cos\alpha=\frac{12}{13}=\frac{b}{c}\\b=12\\c=13[/tex]

Wyliczmy a z twierdzenia Pitagorasa

[tex]a^2+12^2=13^2\\a^2+144=169//-144\\a^2=25\\a=\sqrt{25}=5[/tex]

[tex]sin\alpha=\frac{a}{c}=\frac{5}{13}\\\\tg\alpha=\frac{a}{b}=\frac{5}{12}\\\\ctg\alpha=\frac{12}{5}=2\frac{2}{5}[/tex]

c)

[tex]tg\alpha=\frac{1}{7}=\frac{a}{b}\\a=1\\b=7[/tex]

Wyliczmy c z twierdzenia Pitagorasa

[tex]1^2+7^2=c^2\\1+49=c^2\\c^2=50\\c=\sqrt{50}=5\sqrt{2}[/tex]

[tex]sin\alpha=\frac{a}{c}=\frac{1}{5\sqrt{2}}*\frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{5*2}=\frac{\sqrt{2}}{10}\\\\cos\alpha=\frac{b}{c}=\frac{7}{5\sqrt{2}}*\frac{\sqrt{2}}{\sqrt{2}}=\frac{7\sqrt{2}}{5*2}=\frac{7\sqrt{2}}{10}\\\\ctg\alpha=\frac{b}{a}=\frac{7}{1}=7[/tex]

A) 9

B) wielkopolskie, kujawsko-pomorskie, mazowieckie, podkarpackie, podlaskie, lubelskie, warmińsko-mazurskie,

C) M.Mizeria- 50% głosów czyli 50% z 900 to 450

A.Małosolny - 49% głosów czyli 49% z 900= 441, ponieważ 1% z 900 to 9, 450-9=441

D) woj. Warmińsko-mazurskie- 1012 głosów

70%= 0,7 0,7×1012=708,4 czyli w zaokragleniu 708 głosów

Woj. Wielkopolskie- 1524 głosy

63%=0,63 0,63×1524=960,12 w zaokrągleniu 960 głosów

Więcej osób głosowało na A.Małosolnego w woj. Wielkopolskim.

E) woj. Małopolskie -1020 głosów

1% z 1020 to 10,2

5% z 1020 to 5×10,2=51

To 51 głosów.

F) wzięło udział 15419 osób

15419 - 80%(0,8)

x - 100%

0,8x= 15419 | :0,8

X = 19273,75 w zaokrągleniu 19274 członków THO

G) 53% -głosy A.M.

44% - głosy M.M.

15419 - wszystkich głosów

10% z 15419 to 1541,9

1% z 15419 to 154,19

Głosy A.M.:

5×1541,9=7709,5

3×154,19=462,57

7709,5+462,57=8172,07 w zaokrągleniu 8172 głosy

Głosy M.M.:

4×1541,9=6167,6

4×154,19=616,76

6167,6+616,76=6784,36 w zaokrągleniu 6784 głosów

8172-6784=1388

M.M zdobyła 1388 głosów mniej niż A.M.

Odpowiedź:

1 so shy

2 who helps

3 me neither

4so ambitious

5 really?

6 look like

7very disappointed

8 buying books

C) 20 % figury.

D) 50 % figury.

Pozdrawiam i liczę na naj :)