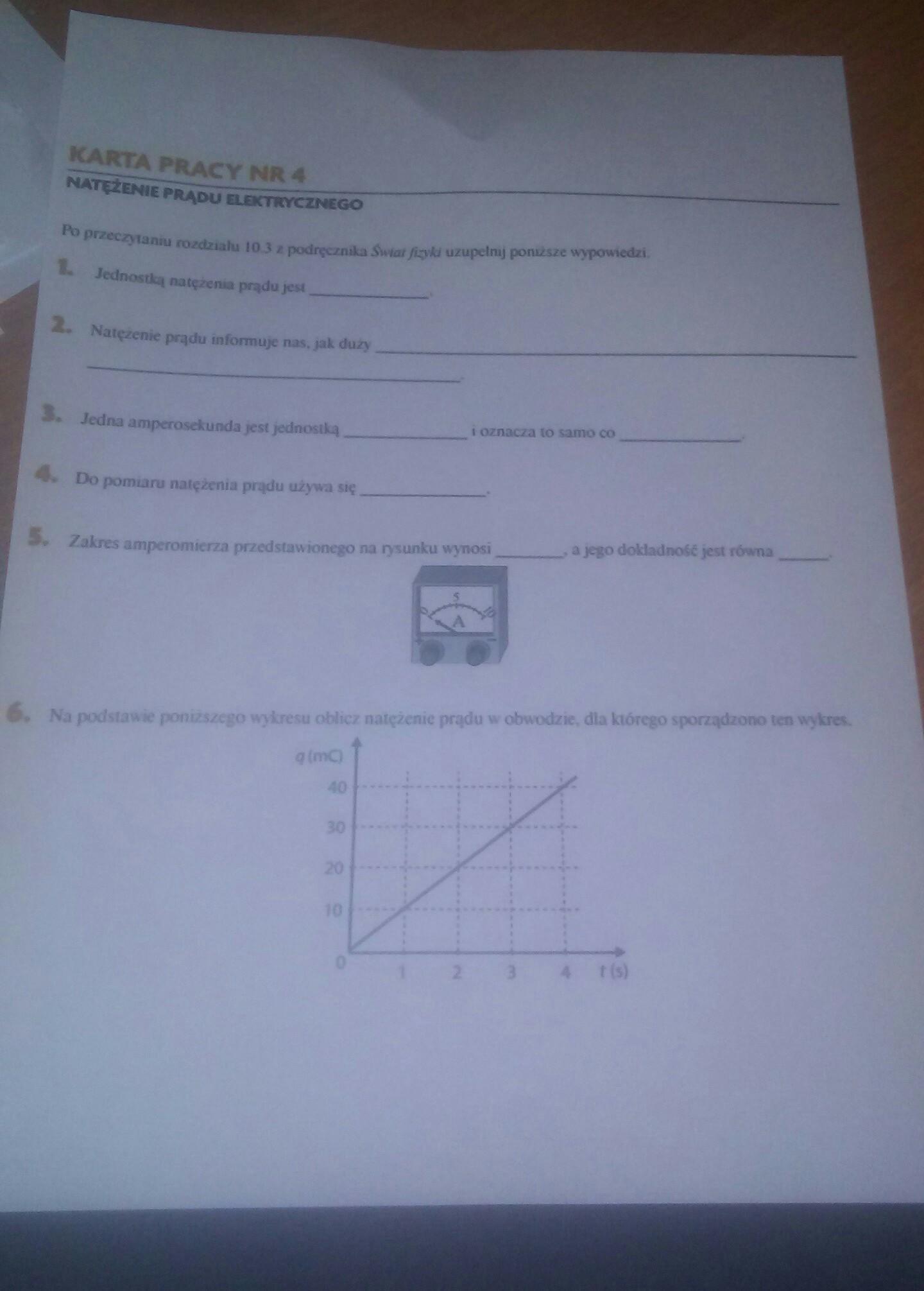
Zadanie 18. (0-2)W kole narysowano cięciwę o długości 10 cm, a jej końce połączono odcinkami ze środkiemkola, tak że powstał trójkąt, którego jeden z kątów ma miarę 120°.Oblicz, jaką długość ma promień tego koła. Zapisz obliczenia.potrzebuje na dzisiaj. Daje naj

Temat:
Matematyka
Autor:
pope97
Utworzono:
1 rok temu

Odpowiedzi 1

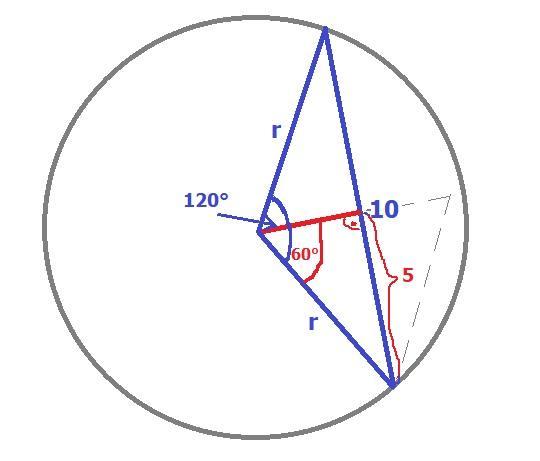
Odcinki łączące końce cięciwy ze środkiem okręgu to promienie (r).

Jeśli w powstałym trójkącie poprowadzimy wysokość ze środka okręgu (rysunek), to podzieli ona kąt 120° na dwa kąty po 60°, a trójkąt na dwa jednakowe trójkąty prostokątne, w których przeciwprostokątnymi są promienie okręgu.

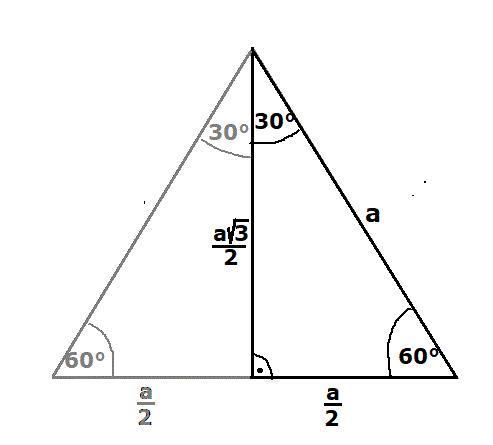
Trójkąt prostokątny o kącie 60° to połówka trójkąta równobocznego (drugi załącznik)

Zatem połowa cięciwy jest wysokością trójkąta równobocznego o boku "r".

Stąd:

[tex]5 = \dfrac{r\sqrt3}2\qquad/\cdot2\\\\10=r\sqrt3\qquad/:\sqrt3\\\\r=\dfrac{10}{\sqrt3}\cdot\dfrac{\sqrt3}{\sqrt3}=\dfrac{10\sqrt3}3\ cm[/tex]

Odp.: Promień okręgu ma długość: [tex]\bold{\dfrac{10\sqrt3}3\ cm}[/tex] {czyli ok. 5,77 cm}

Autor:

williamtwpu
Oceń odpowiedź:
9

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Znajdź w słowniczku obok: 1 pięć nazw zwierząt potrafiących latać, np. fly 2 pięć nazw zwierząt żyjących w środowisku wodnym, np. dolphin 3 pięć przymiotników opisujących pogodę, np. foggy 4 pięć wyrazów/wyrażeń związanych z ochroną środowiska, np. eco-friendly 5 pięć określeń rzeczy zagrażających środowisku naturalnemu, np. global warming