Dla jakich wartości parametru m rozwiązaniem ukladu równań jest paraliczb o przeciwnych znakach?Zadanie 5a i 4b
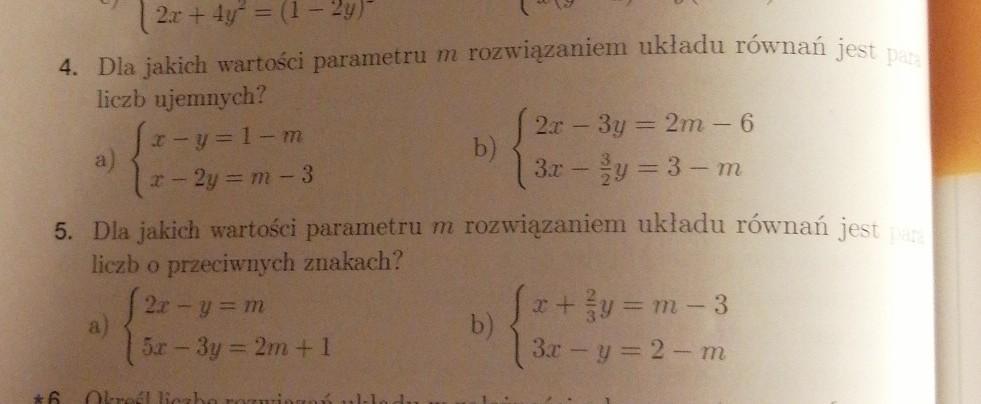
-
Temat:
Matematyka -
Autor:
dexter35 -
Utworzono:
1 rok temu
Odpowiedzi 1
Zad. 4b
[tex]\begin{cases} 2x-3y=2m-6\\ 3x - \frac{3}{2}y= 3 - m \ \ \ |\cdot (-2) \end{cases} \\\\ \underline{\begin{cases} 2x-3y=2m-6\\ -6x +3y= -6+2m \end{cases}} \ \ \ |+ \\\\ - 4x = 2m - 6 - 6+2m \\ -4x = 4m - 12 \ \ \ |:(-4) \\ x = - m +3 \\ x = 3-m \\\\ 2x-3y=2m-6 \\ 2 \cdot (-m + 3) - 3y = 2m -6 \\ -2m +6 -3y= 2m - 6 \\ -3y = 2m - 6 +2m -6 \\ -3y = 4m -12 \ \ \ |:(-3) \\ y = -\frac{4}{3} m +4 \\\\ \begin{cases} x = 3-m \\ y = -\frac{4}{3} m +4 \end{cases}[/tex]
Jeżeli rozwiązaniem układu ma być para liczb ujemnych, to x < 0 i y < 0. Stąd:
[tex]3-m< 0 \ i \ -\frac{4}{3} m +4< 0 \\\\ 3-m< 0 \\ -m < - 3 \ \ \ |\cdot (-1) \\ m > 3 \\\\ -\frac{4}{3} m +4< 0 \\ -\frac{4}{3} m < - 4 \ \ \ |\cdot (-\frac{3}{4}) \\ m > 3 \\\\ Zatem: m > 3, \ czyli \ m \in (3, \ + \infty)[/tex]
Odp. Dla m ∈ (3, + ∞) rozwiązaniem układu równań jest para liczb ujemnych.
Zad. 5a
[tex]\begin{cases} 2x-y=m \ \ \ |\cdot (-3) \\ 5x - 3y = 2m + 1 \end{cases} \\\\ \underline{\begin{cases} -6x+3y=-3m \\ 5x - 3y = 2m + 1 \end{cases}} \ \ \ |+ \\\\ -x=-3m +2m+1 \\ -x = -m + 1 \ \ \ |\cdot(-1) \\ x = m - 1 \\\\ 2x-y=m \\ 2 \cdot (m-1)-y=m \\ 2m - 2 -y = m \\ -y=m -2m +2 \\ -y = - m +2 \ \ \ |\cdot (-1) \\ y = m -2 \\\\ \begin{cases} x = m - 1 \\ y = m - 2 \end{cases}[/tex]
Jeżeli rozwiązaniem ma być para liczb o przeciwnych znakach, to ich iloczyn musi być liczbą ujemną, czyli x · y < 0. Stąd:
(m - 1)(m - 2) < 0
Miejsca zerowe:
(m - 1)(m - 2) = 0
m - 1 = 0 lub m - 2 = 0
m = 1 lub m = 2
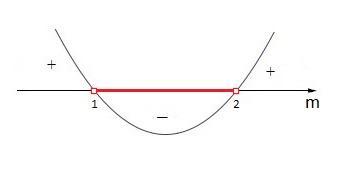
Uwzględniając ostry znak nierówności zaznaczamy miejsca zerowe na osi i rysujemy parabolę z ramionami skierowanymi w górę, bo a = 1 > 0 (rys. w zał.). Z wykresu odczytujemy rozwiązanie nierówności: m ∈ (1, 2)
Odp. Dla m ∈ (1, 2) rozwiązaniem układu równań jest para liczb o przeciwnych znakach.
-
Autor:
chaseo4jk
-
Oceń odpowiedź:
10


