Trójkąt równoboczny ma pole równe 9√3. Prosta równoległa do boku przecina boki i – odpowiednio – w punktach i. Trójkąty i są podobne, a stosunek długości boków tych trójkątów jest równy 3 2. Oblicz długość boku trójkąta.
-
Temat:
Matematyka -
Autor:
natasha70 -
Utworzono:
1 rok temu
Odpowiedzi 1
Myślę, że brakuje części danych w zadaniu. Polecenie powinno brzmieć:
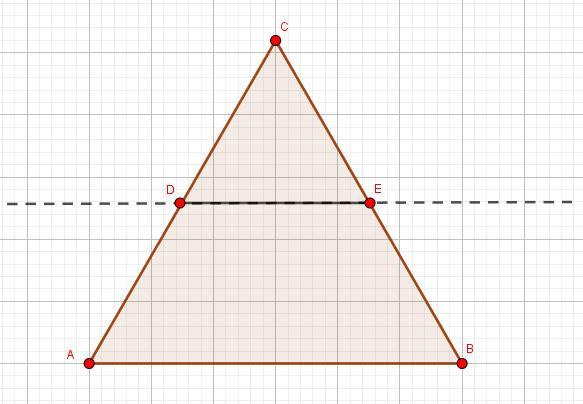
Trójkąt równoboczny ma pole równe 9√3. Prosta równoległa do boku (np. AB) przecina boki AC i BC w punktach odpowiednio D i E. Trójkąty ABC oraz CDE są podobne, a stosunek długości boków tych trójkątów jest równy 3 : 2. Oblicz długość boku trójkąta CDE.
Rysunek pomocniczy w załączniku.
Przypomnijmy wzór na pole trójkąta równobocznego:
[tex]P = P_{\Delta} = \cfrac{a^2\sqrt{3}}{4} \\\\[/tex]
Mając pole trójkąta równobocznego - można wyliczyć długość jego boku.
Dane z zadania:
[tex]P_{\Delta} = 9\sqrt{3} \\\\\cfrac{a^2\sqrt{3}}{4} = 9\sqrt{3} \ | \cdot 4 \\\\a^2\sqrt{3} = 36\sqrt{3} \ | : \sqrt{3} \\\\a^2 = 36 \\\\a = \sqrt{36} = 6[/tex]
Z obliczeń wynika, że długości boków trójkąta ABC wynoszą 6, czyli:
a = |AB| = |BC| = |AC| = 6
Wiemy z treści zadania, że trójkąty ABC i CDE są podobne oraz stosunki długości boków wynoszą 3 : 2. Możemy więc zapisać, że:
[tex]\cfrac{|AB| }{|DE|} = \cfrac{3}{2} \\\\czyli: \\\\\cfrac{6}{|DE| } = \cfrac{3}{2} \\\\[/tex]
Mnożymy na krzyż i otrzymujemy:
[tex]3\cdot |DE| = 6 \cdot 2 \ | :3 \\\\|DE| = 4[/tex]
Jest to również trójkąt równoboczny, więc:
|DE| = |CE| = |CD| = 4
Wniosek: Długość boku trójkąta CDE wynosi 4.
#SPJ4
-
Autor:
kelseylaat
-
Oceń odpowiedź:
4
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
weirdo
-
Autor:
keatonbuwr
-
Oceń odpowiedź:
2
-
Autor:
zoemurphy
-
Autor:
robinijau
-
Oceń odpowiedź:
3
-
Autor:
amandawashington
-
Autor:
cordelld5ic
-
Oceń odpowiedź:
0
-
Autor:
pope97
-
Autor:
billiejenkins
-
Oceń odpowiedź:
8