Zad 3 Dany jest ostroskup prawidłowy czworokątny jak na rysunku 3a Oblicz pole powierzchni całkowitej 3h Oblicz objętość tego ostroskupe​

Na mapie w skali 1:600000 1cm to 600000cm = 6000m = 6km

Czyli 1cm na mapie to 6km

300:6= 50

Odp. D , 50cm to 300km

Odpowiedź:

Szczegółowe wyjaśnienie:

1) D = x ∈ <-5,7>

2) Zw = y ∈ <-2,4>

3) miejsca zerowe: x1 = -3, x2 = 5

4) f(x)↑, dla x ∈ <3,7>

5) f(x)↓, dla x ∈ <-5,-2>

6) f(x)→, dla x ∈ <-2,3>

7) f(x) > 0 dla x ∈ <-5,-3) ∪ (5,7>

8) f(x) < 0 dla x ∈ (-3,5)

I gra muzyka

Pozdrawiam

Skoro sa to ostroslupy prawidlowe, to w postawie maja figury rownoboczne.

[tex]a) \\\text{W postawie kwadrat o boku 4}\\a=4\\b=8\\h_b - \text{wysokosc sciany bocznej}\\H - \text{Wysokosc ostroslupa}\\\\2^2+h_b^2=8^2\\4+h_b^2=64\\h_b^2=60\\h_b=\sqrt{60}=2\sqrt{15}\\\\Pb=4*\frac{ah_b}2=2ah_b=2*4*2\sqrt{15}=16\sqrt{15}j^2\\Pp=a^2=4^2=16j^2\\\\Pc=16\sqrt{15}j^2+16j^2\\\bold{Pc=(16+16\sqrt{15})j^2}\\\\d - \text{przekatna podstawy}\\d=a\sqrt2\\d=4\sqrt2\\(\frac12d)^2+H^2=b^2\\(2\sqrt2)^2+H^2=8^2\\4*2+H^2=64\\8+H^2=64\\H^2=56\\H=\sqrt{56}=2\sqrt{14}\\[/tex]

[tex]V=\frac13Pp*H\\V=\frac13*16j^2*2\sqrt{14}=\frac{32\sqrt{14}j^3}3\\\bold{V=\frac{32\sqrt{14}j^3}3}[/tex]

[tex]b)\\\\\text{W podstawie trojkat rownoboczny}\\h_b=10\\b=12\\(\frac12a)^2+h_b^2=b^2\\\frac14a^2+100=144\\\frac14a^2=44 /*4\\a^2=44*4\\a=\sqrt{4*4*11}=4\sqrt{11}[/tex]

[tex]Pp=\frac{a^2\sqrt3}4\\Pp=\frac{44*4\sqrt3}4=44\sqrt3j^2\\\\Pb=3*\frac{ah_b}2\\Pb=3*\frac{4\sqrt{11}*10}2=12\sqrt{11}*5=60\sqrt{11}\\\\Pc=Pp+Pb=44\sqrt{3}j^2+60\sqrt{11}j^2\\\bold{Pc=(40\sqrt3+60\sqrt{11})j^2}[/tex]

[tex]h_p=\frac{a\sqrt3}2\\h_p=\frac{4\sqrt{11}*\sqrt3}2=2\sqrt{33}\\(\frac23h_p)^2+H^2=b^2\\(\frac23*2\sqrt{33})^2+H^2=144\\(\frac{4}3\sqrt{33})^2+H^2=144\\\frac{16}9*33+H^2=144\\\frac{176}3+H^2=144\\H^2=\frac{432}3-\frac{176}3\\H^2=\frac{256}3\\H=\sqrt{\frac{256}3}=\frac{16}{\sqrt3}=\frac{16\sqrt3}3\\\\V=\frac13Pp*H\\V=\frac13*44\sqrt3j^2*\frac{16\sqrt3}3\\V=\frac{2112}{9}j^3\\\bold{V=\frac{704}3j^3}[/tex]

[tex]c) \\\\\text{W podstawie szesciokat foremny}\\H=9\\\text{Z wlasnosci trojkata o katach 90, 60, 30:}\\b=18\\2a=9\sqrt3/:2\\a=\frac{9\sqrt3}2\\\\Pp=6*\frac{a^2\sqrt3}4=\frac{3a^2\sqrt3}2\\Pp=\frac{3*(\frac{9\sqrt3}2)^2*\sqrt3}2=\frac{3*\frac{81*3}4*\sqrt3}2=\frac{81*9\sqrt3}4*\frac12=\frac{729\sqrt3}8j^2\\\\(\frac12a)^2+h_b^2=b^2\\(\frac12*\frac{9\sqrt3}2)^2+h_b^2=18^2\\(\frac{9\sqrt3}4)^2+h_b^2=324\\\frac{243}{16}+h_b^2=324\\h_b^2=324-\frac{243}{16}\\h_b^2=324-15\frac3{16}\\[/tex]

[tex]h_b^2=323\frac{16}{16}-15\frac3{16}\\h_b^2=308\frac{13}{16}\\h_b^2=\frac{4941}{16}\\h_b=\sqrt{\frac{4941}{16}}=\frac{9\sqrt{61}}{4}\\\\Pb=6*\frac{ah_b}2=3ah_b\\Pb=3*\frac{9\sqrt3}2*\frac{9\sqrt{61}}4=\frac{243*\sqrt{183}}{8}j^2\\\\Pc=Pp+Pb\\Pc=\frac{729\sqrt3}8j^2+\frac{243\sqrt{183}}8j^2\\\bold{Pc=\frac{729\sqrt3+243\sqrt{183}}8j^2}[/tex]

[tex]V=\frac13Pp*H\\V=\frac13*\frac{729\sqrt3}8j^2*9\\\bold{V=\frac{2187\sqrt3}8j^3}[/tex]

Odpowiedź + Szczegółowe wyjaśnienie:

Graniastosłup - bryła posiadająca dwie równoległe podstawy, które są przystającymi wielokątami. Ściany boczne są równoległobokami.

Graniastosłup prosty, to graniastosłup, w którym ściany boczne są prostokątami prostopadłymi do podstaw.

Graniastosłup prawidłowy, to graniastosłup prosty, którego podstawą jest wielokąt foremny. A co za tym idzie, wszystkie ściany boczne są przystającymi prostokątami.

Pp - pole podstawy

Pb - pole powierzchni bocznej

L - obwód podstawy graniastosłupa prostego

H - wysokość graniastosłupa

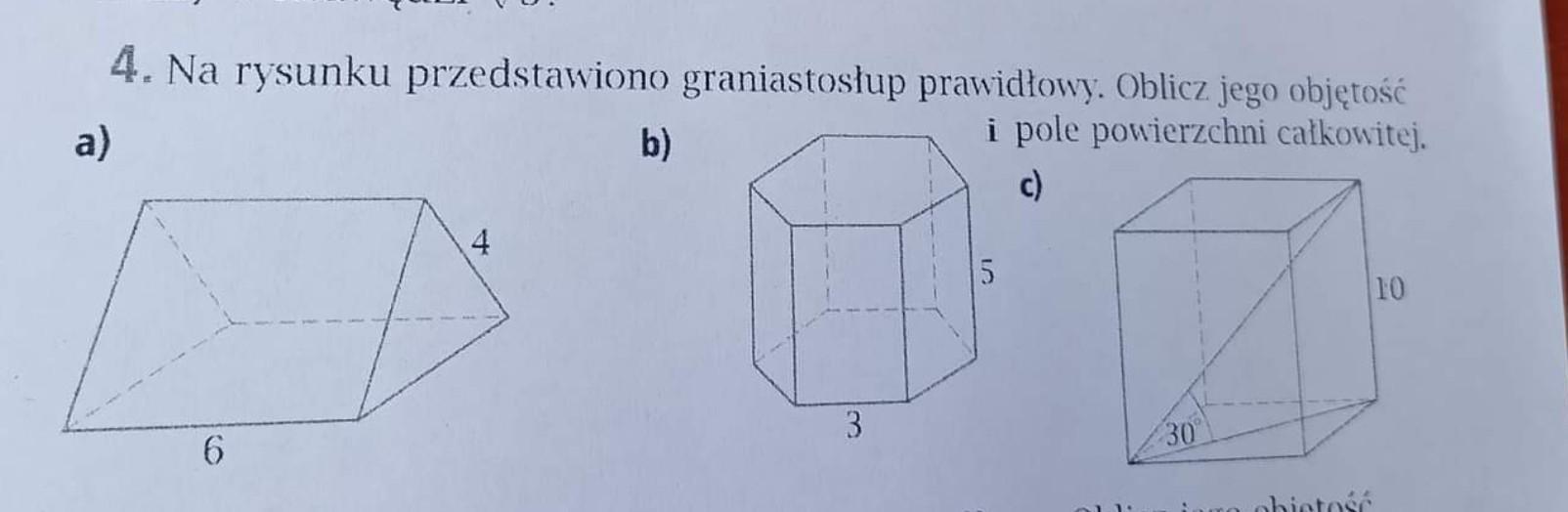
a) Graniastosłup prawidłowy trójkątny (podstawa - trójkąt równoboczny).

a = 4, H = 6

Pp = (4²√3)/4

Pb = (3 · 4) · 6

Pc = 2 · 4√3 + 72

V = 4√3 · 6

b) Graniastosłup prawidłowy sześciokątny (podstawa - sześciokąt foremny)

a = 3, H = 5

Pp = 6 · (3³√3)/4

Pb = (6 · 3) · 5

Pc = 2 · 27√3/2 + 90

V = 27√3/2 · 5

c) Graniastosłup prawidłowy czworokątny (podstawa - kwadrat)

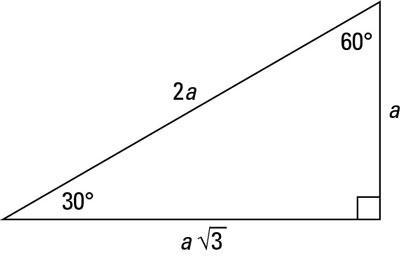
Skorzystamy tutaj z trójkąta prostokątnego o kątach ostrych 30° i 60° (patrz załącznik).

Na podstawie zależności miarowych w takim trójkącie mamy długość przekątnej podstawy (kwadratu):

Wzór na długość przekątnej kwadratu o boku a:

Podstawiamy:

a√2 = 10√3    |·√2

2a = 10√6   |:2

Pp = a²

Pp = (5√6)²

Pp = 5² · (√6)²

Pp = 25 · 6

Pb = (4 · 5√6) · 10

Pc = 2 · 150 + 200√6

V = 150 · 10