prosze o rozwiązanie pozostałych dwóch
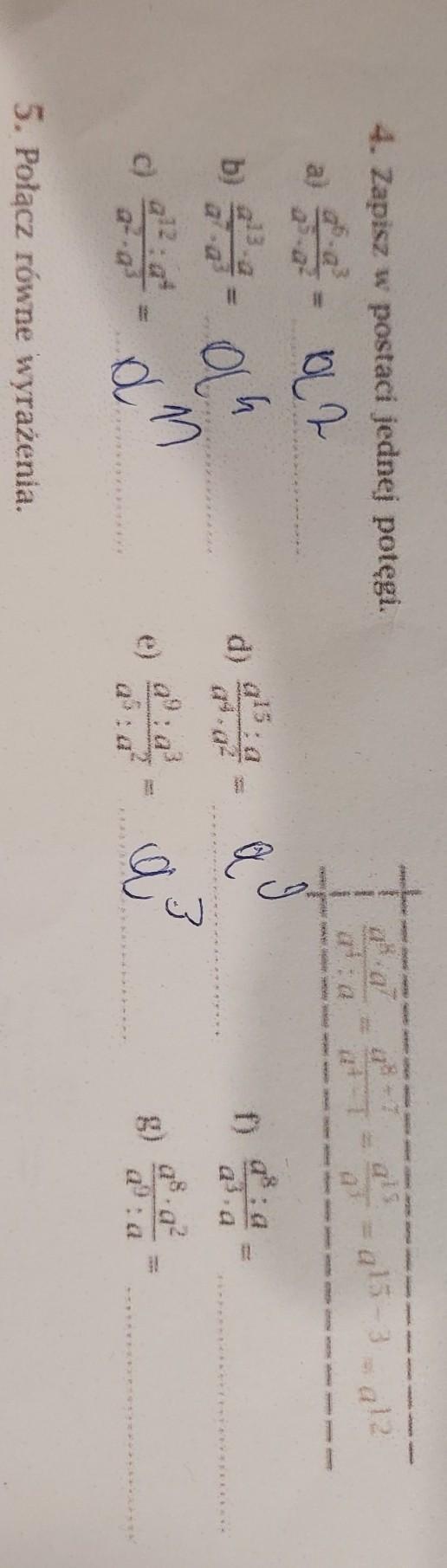
-
Temat:
Matematyka -
Autor:
anthony49 -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
[tex]a)\ \ \dfrac{a^6\cdot a^3}{a^5\cdot a^2}=\dfrac{a^{6+3}}{a^{5+2}}=\dfrac{a^9}{a^7}=a^{9-7}=a^2\\\\\\b)\ \ \dfrac{a^1^3\cdot a}{a^7\cdot a^3}=\dfrac{a^{13+1}}{a^{7+3}}=\dfrac{a^1^4}{a^1^0}=a^{14-10}=a^4\\\\\\c)\ \ \dfrac{a^1^2:a^4}{a^2\cdot a^3}=\dfrac{a^{12-4}}{a^{2+3}}=\dfrac{a^8}{a^5}=a^{8-5}=a^3\\\\\\d)\ \ \dfrac{a^1^5:a}{a^4\cdot a^2}=\dfrac{a^{15-1}}{a^{4+2}}=\dfrac{a^1^4}{a^6}=a^{14-6}=a^8[/tex]
[tex]e)\ \ \dfrac{a^9:a^3}{a^5:a^2}=\dfrac{a^{9-3}}{a^{5-2}}=\dfrac{a^6}{a^3}=a^{6-3}=a^3\\\\\\f)\ \ \dfrac{a^8:a}{a^3\cdot a}=\dfrac{a^{8-1}}{a^{3+1}}=\dfrac{a^7}{a^4}=a^{7-4}=a^3\\\\\\g)\ \ \dfrac{a^8\cdot a^2}{a^9:a}=\dfrac{a^{8+2}}{a^{9-1}}=\dfrac{a^1^0}{a^8}=a^{10-8}=a^2[/tex]
Przy mnożeniu potęg o tych samych podstawach ,podstawę przepisujemy a wykładniki dodajemy , a przy dzieleniu wykładniki odejmujemy
[tex]a^m\cdot a^n=a^{m+n}\\\\a^m:a^n=a^{m-n}[/tex]
-
Autor:
marcelz1x6
-
Oceń odpowiedź:
3


