Oblicz pole trójkąta o wierzchołkach: a) A = (-2, 4), B = (6, -1), C = (2, -1) b) K = (-2, 3), L= (-2, 1), M = (0,0) Z góry dziękuję

Temat:
Matematyka
Autor:
santos82
Utworzono:
1 rok temu

Odpowiedzi 1

I sposób

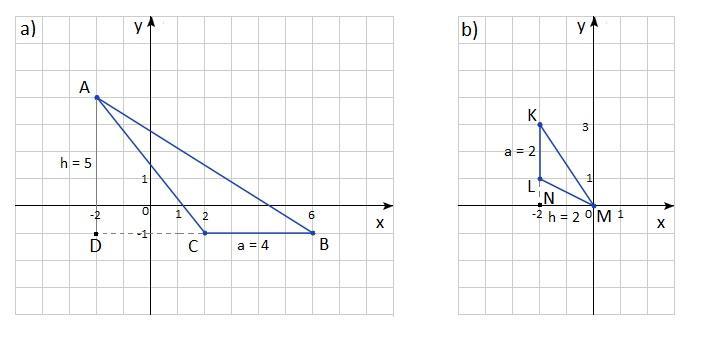
Zaznaczamy wierzchołki trójkąta ABC: A = (- 2, 4), B = (6, - 1), C = (2, - 1) w układzie współrzędnych (rys. a w zał.) i odczytujemy dane do obliczenia pola trójkąta: a = |BC| = 6 - 2 = 4 i h = |AD| = 4 - (- 1) = 4 + 1 = 5

[tex]P_{ABC}= \frac{1}{2} ah = \frac{1}{\not{2}_1} \cdot \not{4}^2 \cdot 5 = 10 \\\\ \boxed{P_{ABC} = 10 \ [j^2]}[/tex]

II sposób

Korzystamy teraz ze wzoru na pole trójkąta o danych wierzchołkach

[tex]A = (x_A, \ y_A), \ B= (x_B, \ y_B), \ C = (x_C, \ y_C)[/tex]:

[tex]P_{ABC}= \frac{1}{2} \cdot |(x_B - x_A)(y_C - y_A) - (y_B - y_A)(x_C - x_A)|[/tex]

----------

[tex]P_{ABC} = \frac{1}{2} \cdot |(6+2)(-1-4) - (-1-4)(2+2)| = \frac{1}{2} \cdot |8 \cdot (-5) - (-5) \cdot 4| = \\ = \frac{1}{2} \cdot |-40 +20| = \frac{1}{2} \cdot |-20| = \frac{1}{\not{2}_1} \cdot \not{20}^{10} = 10 \\\\ \boxed{P_{ABC} = 10 \ [j^2]}[/tex]

I sposób

Zaznaczamy wierzchołki trójkąta KLM: K = (- 2, 3), L = (- 2, 1), M = (0, 0) w układzie współrzędnych (rys. b w zał.) i odczytujemy dane do obliczenia pola trójkąta: a = |KL| = 3 - 1 = 2 i h = |MN| = 0 - (- 2) = 0 + 2 = 2

[tex]P_{KLM}= \frac{1}{2} ah = \frac{1}{\not{2}_1} \cdot \not{2}^1 \cdot 2 = 2 \\\\ \boxed{P_{KLM} = 2 \ [j^2]}[/tex]

II sposób

Korzystamy teraz ze wzoru na pole trójkąta o danych wierzchołkach:

[tex]P_{KLM}= \frac{1}{2} \cdot |(-2 +2)(0 - 3) - (1 - 3)(0 +2)|= \frac{1}{2} \cdot |0 \cdot (- 3) - (-2) \cdot 2|= \\ = \frac{1}{2} \cdot |0 +4|= \frac{1}{\not{2}_1} \cdot \not{4}^2=2 \\\\ \boxed{P_{KLM} = 2 \ [j^2]}[/tex]

Autor:

jackhxqv
Oceń odpowiedź:
9

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Ustal i zapisz, jaką częścią mowy jest każdy wyraz w zdaniach. SAMURAJOWIE STANOWILI DZIESIĘĆ PROCENT SPOŁECZEŃSTWA. CIESZYLI SIĘ SPECJALNYMI PRZYWILEJAMI, A ICH SŁUŻBA BYŁA CZĘSTO NIEBEZPIECZNA. plzz potrzebuję na teraz

Autor:

branden

Autor:

earlbb3d
Oceń odpowiedź:
0

Dam naj!! pomocy na dziś!! W przywołanym fragmencie książkiJacka Dukaja (patrz: s. 9) wskażelementy świata przedstawionego, któretraktujesz jako ci bliskie, znajome, orazte, które możesz określić jako obce,pochodzące z innego świata niż twoj.

Autor:

carolina32

Autor:

jettazkys
Oceń odpowiedź:
0

a) Dokończ zdanie. Wybierz odpowiedź A albo Bijej uzasadnienie 1., 2. lub 3.Dzięki osobie oznaczonej literą A siedzącej obok Józefa Piłsudskiego polskie władzezyskały uznanie1.A.państwententy,działał na rzecz sprawy polskiej w StanachZjednoczonych i Europie Zachodniej.w trakcie I wojny światowej współpracował z rządemaustriackim.ponieważpolityk ten2.B.państwcentralnych,3.współdziałał z Ignacym Daszyńskim w tworzeniuTymczasowego Rządu Ludowego Republiki Polskiej.

Autor:

kayleighcarr

Autor:

jakob148
Oceń odpowiedź:
10

Daje naj potrzebuje na dzisiaj

Autor:

loosetooth

Autor:

barkleyralc
Oceń odpowiedź:
20

Oblicz pole trójkąta o wierzchołkach: a) A = (-2, 4), B = (6, -1), C = (2, -1) b) K = (-2, 3), L= (-2, 1), M = (0,0) Z góry dziękuję

Odpowiedzi 1

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Other Matematyka Questions