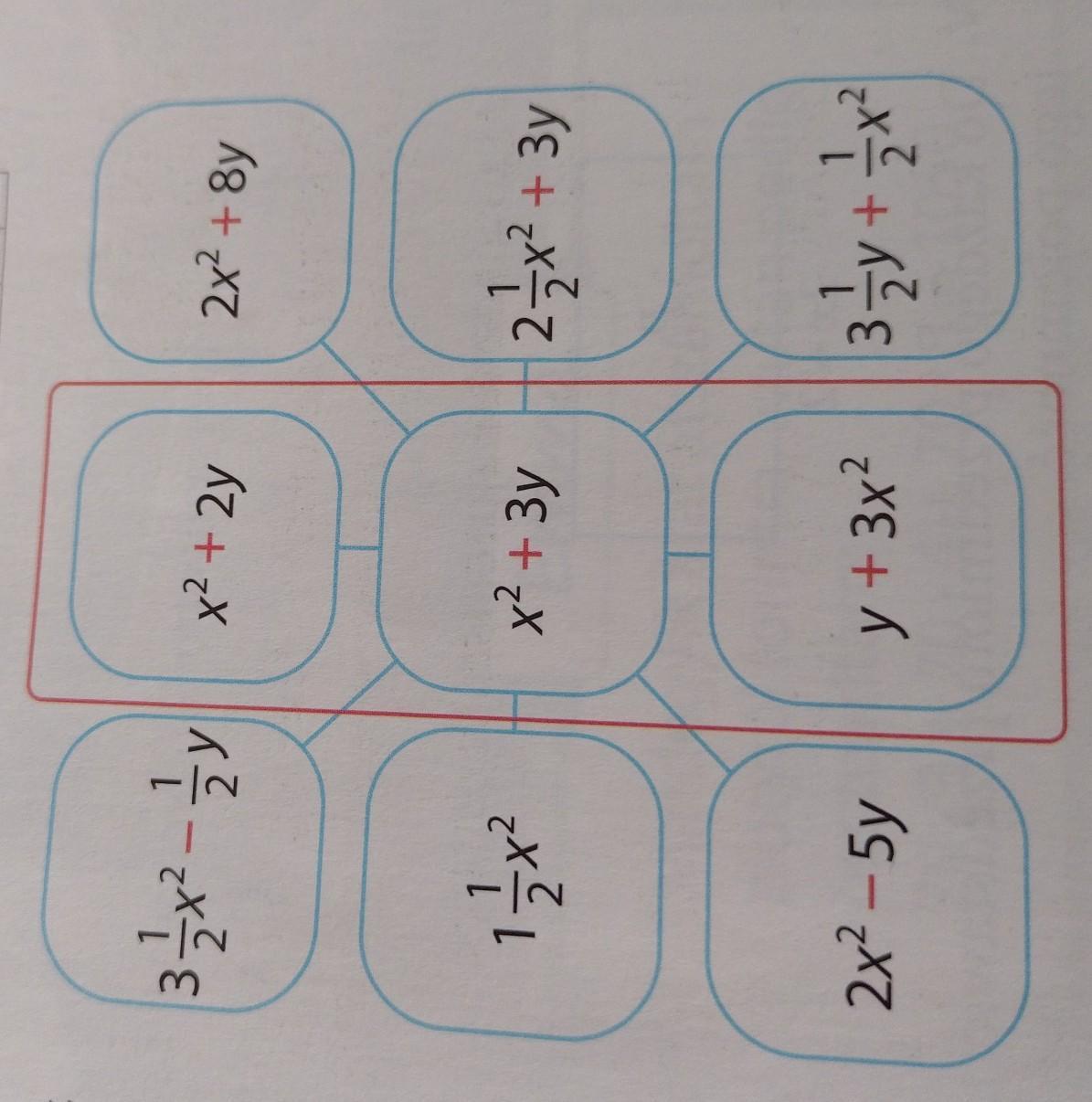
5. Rozpatrz sumy wyrażeń leżących wzdłuż tej samej linii (rysunek obok), np. x² + 2y + x² + 3y + x + 3y + y + 3x? Sprawdź, czy wszystkie te sumy są równe. klasa 7proszę o szybką odpowiedź

Temat:
Matematyka
Autor:
cayo
Utworzono:
1 rok temu

Odpowiedzi 1

Sprawdźmy, czy wszystkie sumy wyrażeń wzdłuż tej samej linii są takie same. Okazuje się, sumy wyrazów leżących w tej samej linii nie są sobie równe.

Istnieje osiem takich sum:

1) [tex]3\frac{1}{2}x^2-\frac{1}{2}y+1\frac{1}{2}x^2+2x^2-5y=7x^2-5\frac{1}{2}y[/tex]

2) [tex]x^2+2y+x^2+3y+y+3x^2=5x^2+6y[/tex]

3) [tex]2x^2+8y+2\frac{1}{2}x^2+3y+3\frac{1}{2}y+\frac{1}{2}x^2=5x^2+14\frac{1}{2}y[/tex]

4) [tex]3\frac{1}{2}x^2-\frac{1}{2} y+x^2+2y+2x^2+8y=6\frac{1}{2}x^2+9\frac{1}{2}y[/tex]

5) [tex]1\frac{1}{2}x^2+x^2+3y+2\frac{1}{2} x^2+3y=5x^2+6y[/tex]

6) [tex]2x^2-5y+y+3x^2+3\frac{1}{2} y+\frac{1}{2}x^2=5\frac{1}{2} x^2-\frac{1}{2}y[/tex]

7) [tex]3\frac{1}{2}x^2-\frac{1}{2}y+x^2+3y+3\frac{1}{2}y+\frac{1}{2}x^2=5x^2+6y[/tex]

8) [tex]2x^2-5y+x^2+3y+2x^2+8y=5x^2+6y[/tex]

Autor:

benjaminks00
Oceń odpowiedź:
2

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

13. Nie mierząc długości boków, oblicz obwody poniższych wielokątów. 5 cm 54 mm Obwód = Obwód =Błagam pomocy!

Autor:

bass

Autor:

siennaaok7
Oceń odpowiedź:
4

Zaznacz wszystkie zdania opisujące sytuację na froncie zachodnim w latach 1915–1917. tym okresie obie strony przeprowadziły dwie wielkie ofensywy, które zakończyły się rzezią uczestniczących w nich żołnierzy i niewielkimi zmianami na linii frontu. Po powstrzymaniu natarcia Niemców w bitwie pod Marną siły państw centralnych przeszły do wojny manewrowej. W pierwszym okresie działań zbrojnych Niemcy realizowały koncepcję wojny pozycyjnej. USA przystąpiły do wojny po stronie państw ententy. Wobec pogarszającej się sytuacji militarnej państw centralnych Niemcy podjęły decyzję o ogłoszeniu nieograniczonej wojny podwodnej