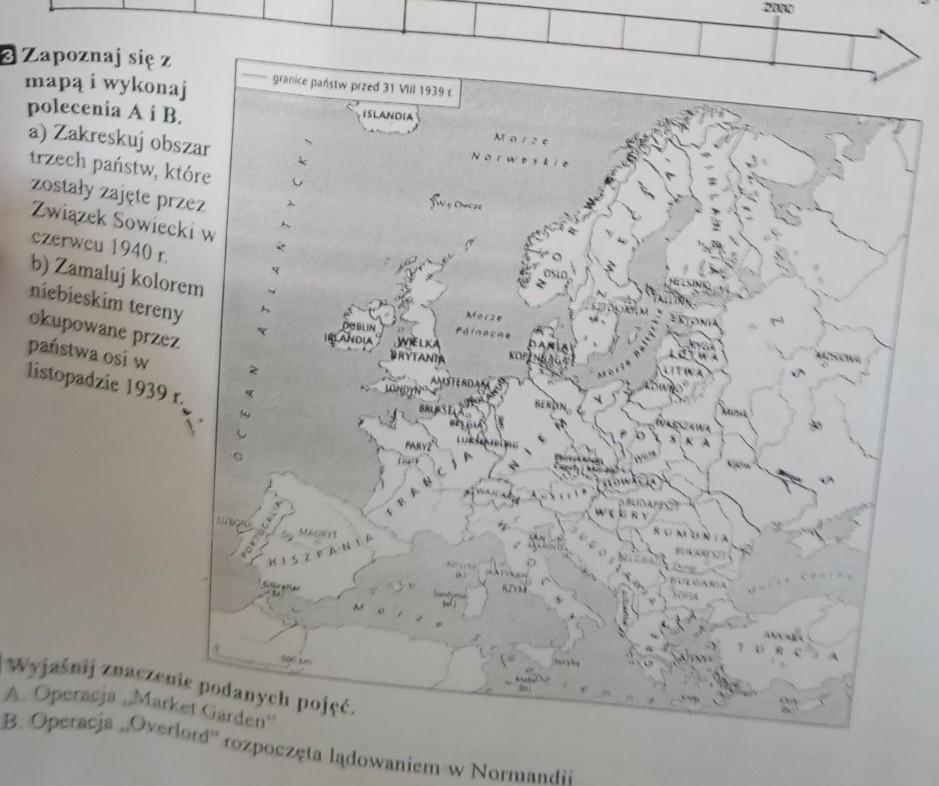
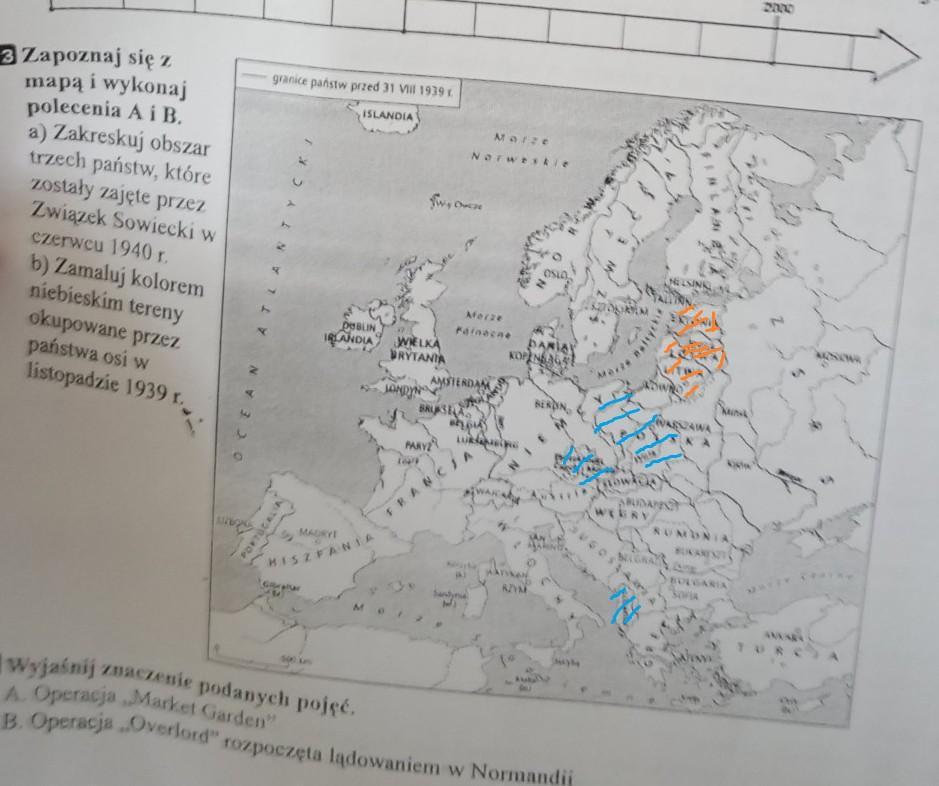
Na boku AB trójkąta ABC wybrano punkt D, a na boku AC - punkt E w taki sposób, że odcinek DE jest równoległy do odcinka BC. Oblicz długość odcinka AD, jeżeli |DB|=4, |AC|= 10, |AE|= 5.
-
Temat:
Matematyka -
Autor:
coltonbutler -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
Szczegółowe wyjaśnienie:
Trójkąty ABC i ADE sa podobne (kkk, równe kąty z tw Talesa), czyli boki sa proporcjonalne, wsp. proporcjonalności:
k = AC/AE = 10/5 = 2
czyli również :
(AD+DB)/AD = 2 czyli:
(AD+4)/AD = 2
AD+4 = 2*AD
AD = 4
-
Autor:
victoriaxtuw
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years