Podstawy trapezu ABCD mają długość: |AB|= 6 cm i |DC|= 3 cm. Ramiona przedłużono do przecięcia się w punkcie P. Wiedząc, że suma długości ramion trapezu jest równa 7 cm, oblicz obwód trójkąta DCP.
-
Temat:
Matematyka -
Autor:
camillamelton -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
L = 10cmSzczegółowe wyjaśnienie:
Rysunek poglądowy w załączniku.
Wiemy, że trójkąty ABP i DCP są podobne na podstawie cechy podobieństwa Kąt-Kąt-Kąt (jeżeli kąty jednego trójkąta mają takie same miary co kąty drugiego trójkąta, to takie trójkąty są podobne).
Jeżeli trójkąty są podobne, to stosunek długości odpowiadających sobie boków jest stały i jest nazywany skalą podobieństwa.
W danych trójkątach odpowiadające sobie boki to AB i DC.
Obliczamy skalę podobieństwa k mniejszego trójkąta do większego:
k = |DC|/|AB|
k = 3/6
k = 1/2Czyli wszystkie boki trójkąta DCP stanowią połowę długości boków trójkąta ABP.
Stąd mamy równania:
|DP| = 1/2|AP||CP| = 1/2|BP|Podstawiamy:
|DP| = a
|CP| = b
|AP| = x + a
|BP| = y + a
a = 1/2(x + a)
b = 1/2(y + b)
a = 1/2x + 1/2a |-1/2a
b = 1/2y + 1/2b |-1/2b
1/2a = 1/2x |·2
1/2b = 1/2y |·2
a = xb = yStąd
x + y = 7 ⇒ a + b = 7Ostatecznie obwód trójkąta DCP wynosi:
L = 3 + 7 = 10(cm)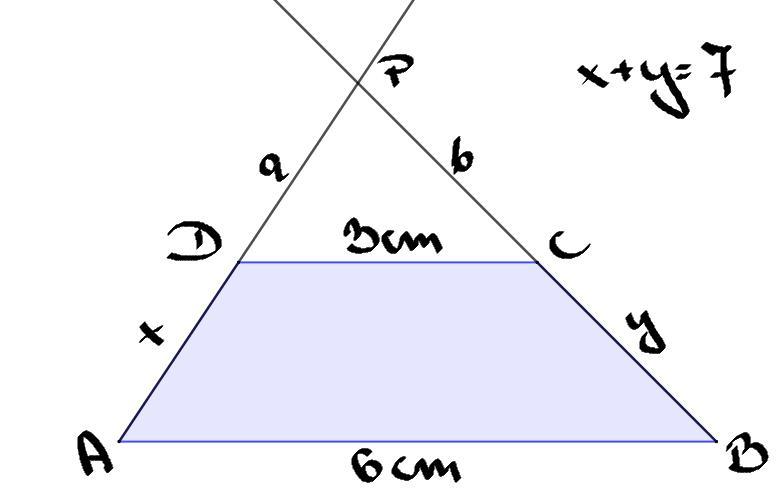
-
Autor:
micah6yx0
-
Oceń odpowiedź:
4


