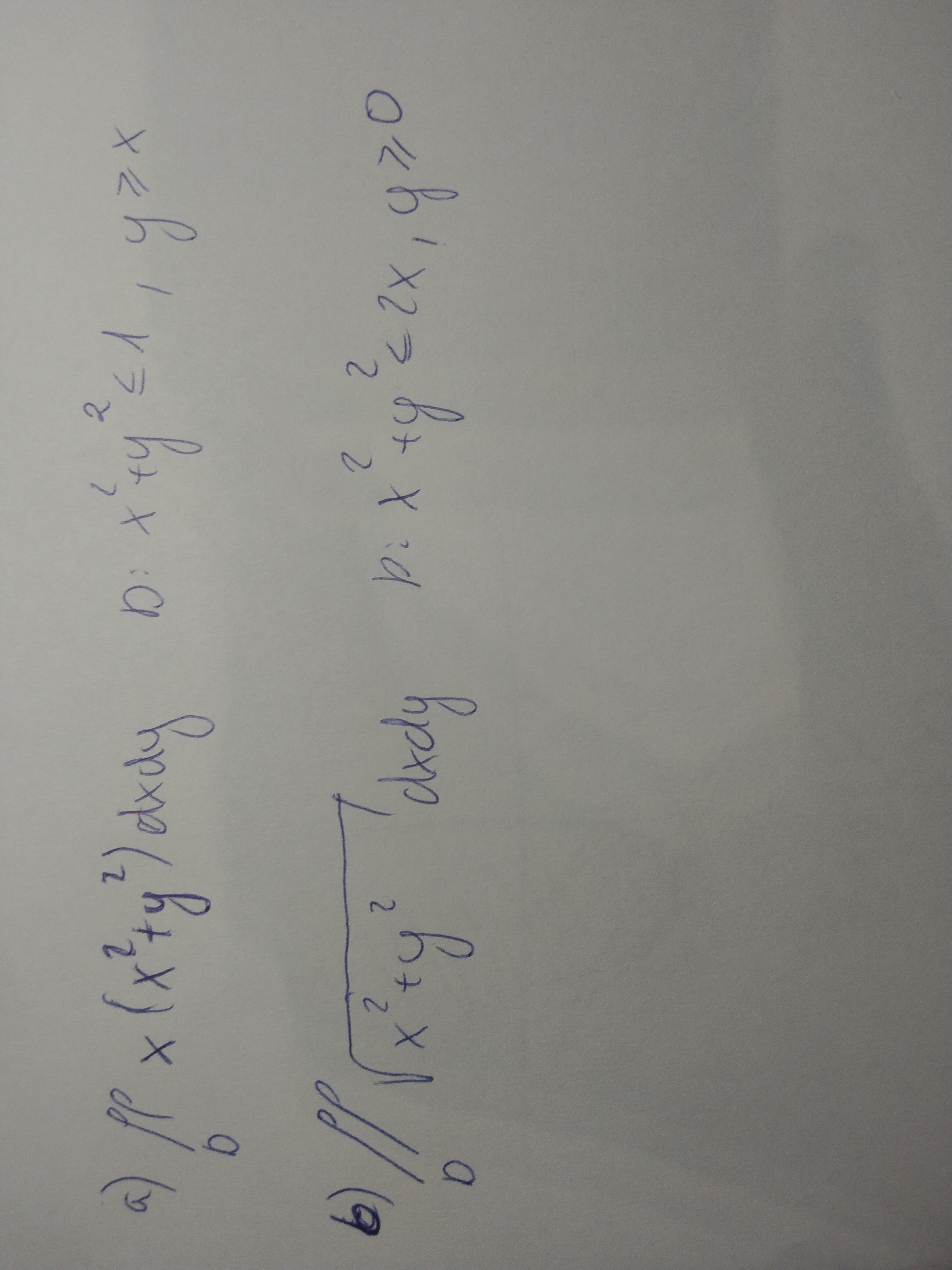Marcel co roku wydaje na książki średnio 220 zł, czyli 44% rocznej sumy swojego kieszonkowego. Ile wynosi ta suma?.

Odpowiedź:

W średniowieczu używało się słowa chirurg, medyk, znachor lub doktor plagi zamiast lekarz.

Wyjaśnienie:

Odpowiedź:

Lekarz w średniowieczu to= medyk.

Wyjaśnienie:

Odpowiedź:

łęta

Wyjaśnienie:

Odpowiedź:

a + ( a + 3) + ( a - 7) = 3 a + 3 - 7 = 3 a - 4

Szczegółowe wyjaśnienie:

Rozwiązanie:

[tex]\bold{(a)}[/tex]

[tex]$\iint \limits^{}_{D}x(x^{2}+y^{2})dxdy[/tex]

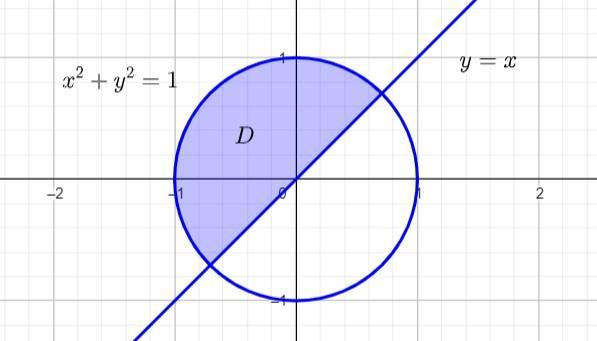
[tex]D=\{(x,y) \in \mathbb{R}^{2}:x^{2}+y^{2}\leq 1 \wedge y\geq x\}[/tex]

Rysunek w załączniku.

Współrzędne biegunowe:

[tex]$\left \{ {{x=r\cos \varphi} \atop {y=r\sin \varphi}} \right.[/tex]

[tex]J(r, \varphi)=r[/tex]

gdzie:

[tex]0\leq r\leq 1[/tex]

[tex]$\frac{\pi}{4}\leq \varphi \leq \frac{5\pi}{4}[/tex]

Całka:[tex]$\iint \limits^{}_{D}x(x^{2}+y^{2})dxdy=\int\limits^{1}_{0}\Bigg(\int \limits^{\frac{5\pi}{4}}_{\frac{\pi}{4}} r\cos \varphi \cdot r^{2} \cdot r \ d \varphi\Bigg)dr=\int\limits^{1}_{0}\Bigg(\int \limits^{\frac{5\pi}{4}}_{\frac{\pi}{4}} r^{4}\cos \varphi \ d \varphi\Bigg)dr=[/tex]

[tex]$=\int\limits^{1}_{0}r^{4} \cdot \sin \varphi \Bigg|^{\frac{5\pi}{4}}_{\frac{\pi}{4}} \ dr=-\sqrt{2}\int\limits^{1}_{0} r^{4} \ dr=-\sqrt{2} \cdot \frac{r^5}{5}\Bigg|^{1}_{0}=-\frac{\sqrt{2}}{5}[/tex]

[tex]\bold{(b)}[/tex]

[tex]$\iint \limits^{}_{D}\sqrt{x^{2}+y^{2}} \ dxdy[/tex]

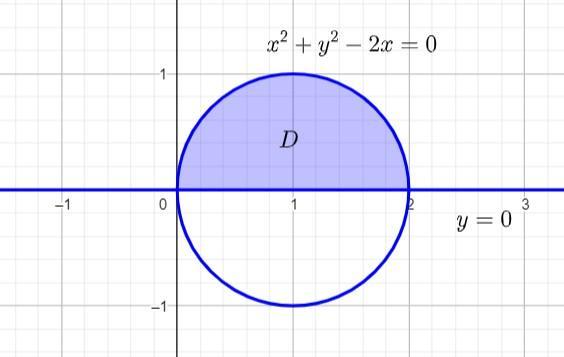
[tex]D=\{(x,y) \in \mathbb{R}^{2}: x^{2}+y^{2}\leq 2x \wedge y \geq 0\}[/tex]

Rysunek w załączniku.

Okrąg:

[tex]x^{2}+y^{2}\leq 2x \iff (x-1)^{2}+y^{2}\leq 1[/tex]

Współrzędne biegunowe:

[tex]$\left \{ {{x=r\cos \varphi} \atop {y=r\sin \varphi}} \right.[/tex]

[tex]J(r, \varphi)=r[/tex]

Z rysunku łatwo odczytać tylko zmianę kąta [tex]\varphi[/tex] :

[tex]$0 \leq \varphi\leq \frac{\pi}{2}[/tex]

Zmianę promienia obliczamy korzystając z podanych nierówności:

[tex]x^{2}+y^{2}\leq 2x[/tex]

[tex]r^{2}\cos^{2}\varphi +r^{2}\sin^{2} \varphi\leq 2r\cos \varphi[/tex]

[tex]r^{2}\leq 2r\cos \varphi[/tex]

Wiemy, że [tex]r\geq 0[/tex], a więc dzielimy obustronnie przez [tex]r[/tex] :

[tex]r\leq 2 \cos \varphi[/tex]

Ostatecznie:

[tex]0\leq r\leq 2 \cos \varphi[/tex]

Całka:

[tex]$\iint \limits^{}_{D}\sqrt{x^{2}+y^{2}} \ dxdy=\int \limits^{\frac{\pi}{2}}_{0}\Bigg(\int\limits^{2\cos \varphi}_{0} \sqrt{r^{2}} \cdot r \ dr \Bigg)d \varphi=\int \limits^{\frac{\pi}{2}}_{0}\Bigg(\int\limits^{2\cos \varphi}_{0} r^{2}\ dr \Bigg)d \varphi=[/tex]

[tex]$=\int\limits^{\frac{\pi}{2}}_{0} \frac{r^{3}}{3} \Bigg|^{2 \cos \varphi}_{0} \ d \varphi=\frac{8}{3}\int \limits^{\frac{\pi}{2}}_{0}\cos^{3} \varphi \ d \varphi=\frac{8}{3} \Big(\sin \varphi - \frac{\sin^{3} \varphi}{3}\Big)\Bigg|^{\frac{\pi}{2}}_{0}=\frac{16}{9}[/tex]