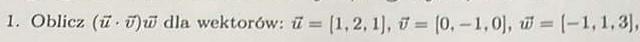sprawdz czy podana formuła logiczna jest tatuologia `(p^q)<=>[(`p)v(`q)]
-
Temat:
Matematyka -
Autor:
kristopher -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
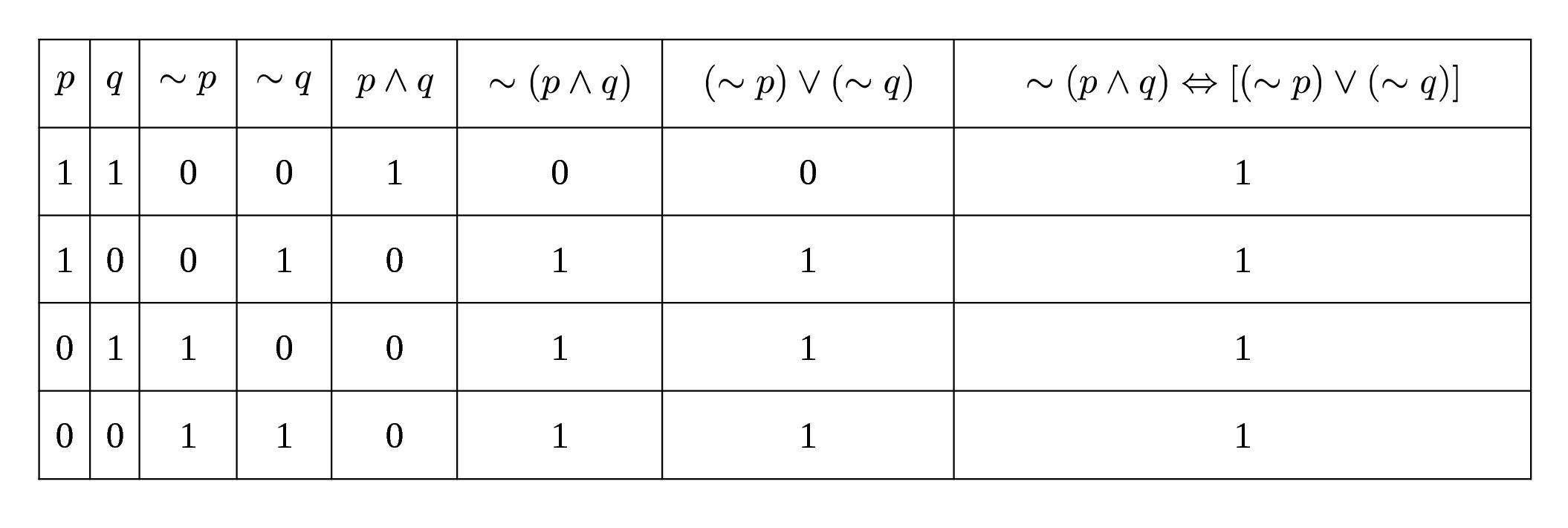
Na podstawie tablicy prawdy (w załączniku) to jest tautologia.
Szczegółowe wyjaśnienie:
-
Autor:
maverick8dje
-
Oceń odpowiedź:
1
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years