Zapisz pole narysowanej figury w postaci sumy algebraicznej. Przy podstawie trójkąta jest 3x-2. Bardzo proszę o pomoc. Daje 20 punktów. ​

Odpowiedź:

poprawne to 1 i 3

Wyjaśnienie:

licze na naj..

Odpowiedź:

w załączniku odpowiedź

Wyjaśnienie:

Odpowiedź:

Bitwa pod Grunwaldem zakończyła się zwycięstwem wojsk polsko-litewskich i pogromem sił krzyżackich, nie została jednak wykorzystana dla całkowitego zniszczenia zakonu. Dzięki zwycięstwu Jagiełło pozyskał większe zaufanie polskiej szlachty, przez co umocnił swoją pozycję na tronie królewskim.

Odpowiedź:

1.Jagiełło pozyskał większe zaufanie polskiej szlachty, przez co umocnił swoją pozycję na tronie królewskim.

2.Zakon krzyżacki został podłamany, dzięki czemu nie stanowił już zagrożenia zbrojnego

Odpowiedź:

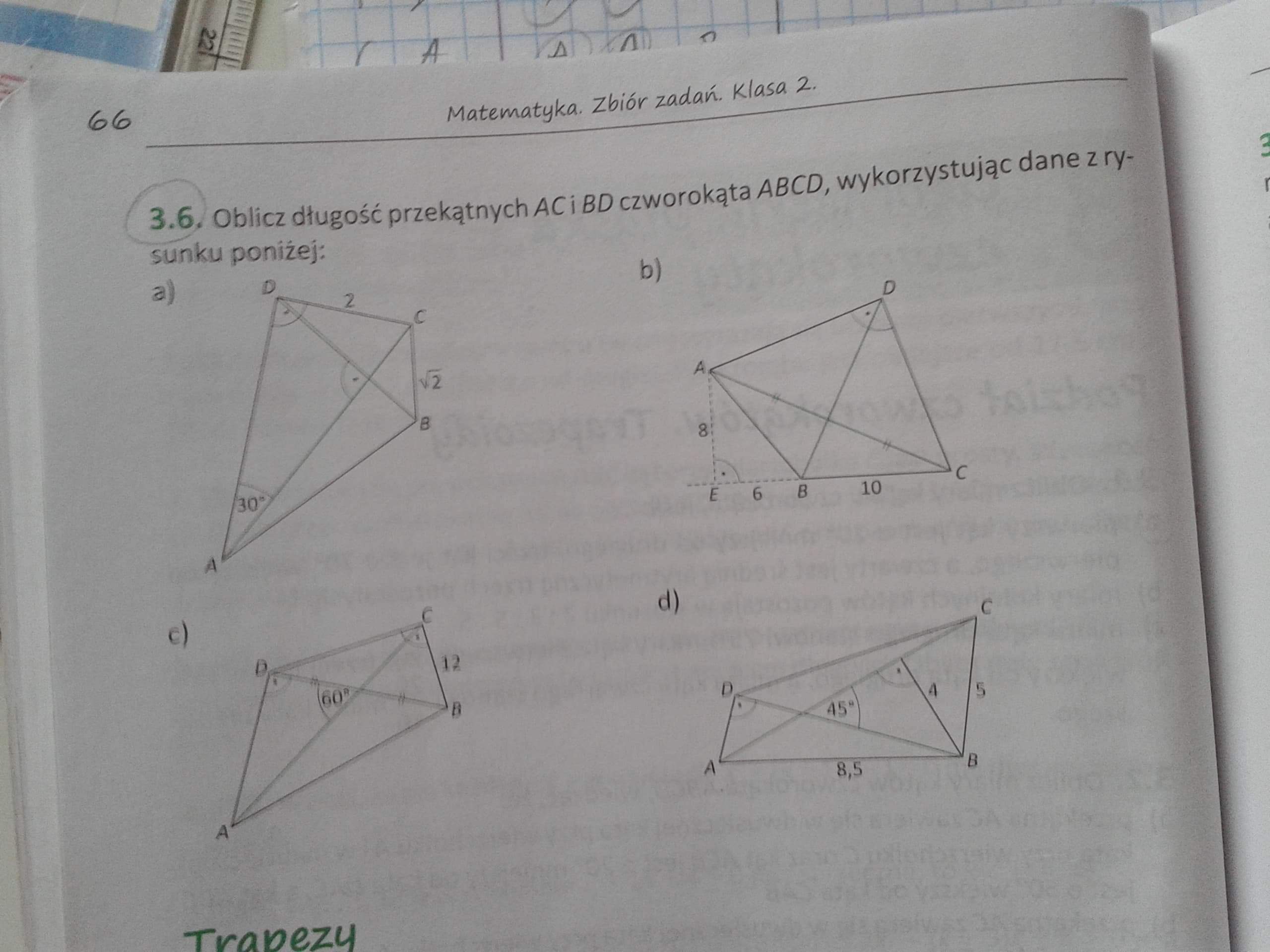
a) Korzystając ze związków w trójkącie o kątach 30°, 60°, 90° otrzymujemy:

|AC| = 2|DC| = 4

Oznaczamy punkt przecięcia przekątnych przez O.

Kąty wierzchołkowe są sobie równe czyli trójkąty DCO oraz BCO są prostokątne.

Co więcej trójkąt DCO ma jeden z kątów równy 30 (kąt przy wierzchołku D).

Z własności tego trójkąta prostokątnego o kątach 30°, 60°, 90° otrzymujemy:

|CO| = [tex]\frac{1}{2}[/tex]|DC| = 1

|DO| = [tex]\sqrt{3}[/tex]

Z tw. Pitagorasa:

|BO|² = [tex]\sqrt{2}[/tex]² - 1² = 1

|BO| = 1

|DB| = [tex]\sqrt{3}[/tex] + 1

b)

Z tw. Pitagorasa:

|AC|² = 8² + (10 + 6)² = 64 + 256 = 320

|AC| = 8[tex]\sqrt{5}[/tex]

x² = 8² + 6² = 100

x = 10

Oznaczamy przez O punkt przecięcia przekątnych.

|BO|² = 10² - ([tex]\frac{1}{2}[/tex] · 8[tex]\sqrt{5}[/tex])² = 100 - 80 = 20

|BO| = 2[tex]\sqrt{5}[/tex]

Zauważ że trójkąt DOC jest równoramienny.

|DO| = [tex]\frac{1}{2}[/tex] |AC| = 4[tex]\sqrt{5}[/tex]

|DB| = 4[tex]\sqrt{5}[/tex] + 2[tex]\sqrt{5}[/tex] = 6[tex]\sqrt{5}[/tex]

c)

|OB| = 12

|DB| = 24

|CO| = 12

Z własności trójkątów prostokątnych o boku 30° :

|AO| = 2 · 12 = 24

|AC| = 12 + 24 = 36

d)

|OB| = 4[tex]\sqrt{2}[/tex]

|OX| = 4

|XC|² = 5² - 4² = 9

|XC| = 3

Zauważ że trójkąt DAO jest prostokątny i równoramienny.

|AD| = y

(8,5)² = y² + (y + 4[tex]\sqrt{2}[/tex])²

[tex]\frac{289}{4}[/tex] = y² + y² + 8y[tex]\sqrt{2}[/tex] + 32

8y² + 32y[tex]\sqrt{2}[/tex] + 128 - 289 = 0

8y² + 32y[tex]\sqrt{2}[/tex] - 161 = 0

Δ = 7200

√Δ = 60[tex]\sqrt{2}[/tex]

[tex]y_{1}[/tex] = [tex]\frac{-32\sqrt{2} - 60\sqrt{2}}{16}[/tex]  < 0

[tex]y_{2}[/tex] = [tex]\frac{-32\sqrt{2} + 60\sqrt{2}}{16}[/tex] = [tex]\frac{7}{4}[/tex] · [tex]\sqrt{2}[/tex]

|BD| = [tex]\frac{7}{4}[/tex] · [tex]\sqrt{2}[/tex] + 4[tex]\sqrt{2}[/tex] = [tex]\frac{23\sqrt{2}}{4}[/tex]

|AO| = y[tex]\sqrt{2}[/tex] = [tex]\frac{7}{4}[/tex] · [tex]\sqrt{2}[/tex] · [tex]\sqrt{2}[/tex] = [tex]\frac{7}{2}[/tex]

|AC| = [tex]\frac{7}{2}[/tex] + 7 = 10[tex]\frac{1}{2}[/tex]