Uważnie budujemy interwały tercji pamiętając słowa piosenki"tercja wielka całe tony mieści dwacały ton i półton tercja mała ma,tercja to odległość stopni trzecha tercjowy walczyk łatwa rzecz " :) prosze daje naj

question img

Odpowiedzi 1

mam nadzieje, ze pomoglam

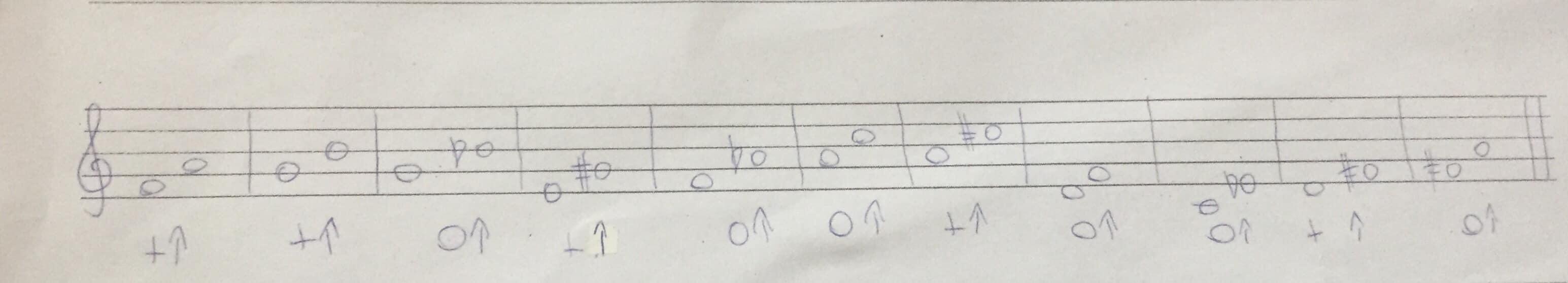
answer img

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Jaką zmianę wprowadził dyrektor Kriestoobriadnikow? A. Zamknął stancje prowadzone przez Polaków. B. Nakazał nauczycielom regularne kontrolowanie stancji. C. Pozwolił gimnazjalistom na czytanie polskich książek. D. Zaostrzył kary dla uczniów łamiących wprowadzone zasady.
nie jestem pewna bo dawno ale chyba B
Zadanie umieszczone powyżej. Zad. 3. str. 70 geografia klasa 7 . Proszę o zdjęcie jeśli można. Podręcznik strona 106-108 te mapy można znaleść również w internecie. Z góry dziękuję. DAJĘ NAJ ​
question img

Odpowiedź:

Juchnowiec Kościelny                                            Dubicze Cerkiewne

15% (promila)                                                                  poniżej  -6--3

powyżej 10%                                                                   poniżej -10

12%                                                                                     40%

PS. Robiliśmy z panią na lekcji to powinno być dobrze

answer img
Dokończ zdanie. spośród podanych odpowiedzi wybierz poprawną. ​
question img

Odpowiedź:

Chyba B. C i D napewno nie

Korzystając ze wzorów Viete'a oblicz: a) x1 kwadrat + x2 kwadrat b) 1/x1 + 1/x2 Proszę o szybką pomoc

Wzory Viete'a: [tex]x_1+x_2=\frac{-b}{a}, x_1x_2=\frac{c}{a}[/tex]

a) chcemy mieć sumę [tex]x_1^2[/tex] i [tex]x_2^2[/tex], więc użyjemy wzoru na sumę pierwiastków i podniesiemy obie strony do kwadratu.

[tex](x_1+x_2)^2=(\frac{-b}{a})^2\\x_1^2+2x_1x_2+x_2^2=\frac{b^2}{a^2}[/tex], wiemy, że [tex]x_1x_2=\frac{c}{a}[/tex], więc podstawiamy

[tex]x_1^2+2\frac{c}{a}+x_2^2=\frac{b^2}{a^2}\\x_1^2+x_2^2=\frac{b^2}{a^2}-\frac{2c}{a}[/tex]

b) sprowadźmy wpierw wyrażenie do wspólnego mianownika

[tex]\frac{1}{x_1} +\frac{1}{x_2} =\frac{x_2}{x_1x_2} +\frac{x_1}{x_1x_2} =\frac{x_1+x_2}{x_1x_2}[/tex] i podstawiamy wzory Viete'a

[tex]\frac{x_1+x_2}{x_1x_2}=\frac{\frac{-b}{a}}{\frac{c}{a}}=\frac{-b}{c}[/tex]

Other Muzyka Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years