Napisze mi ktoś chwyty na flet?

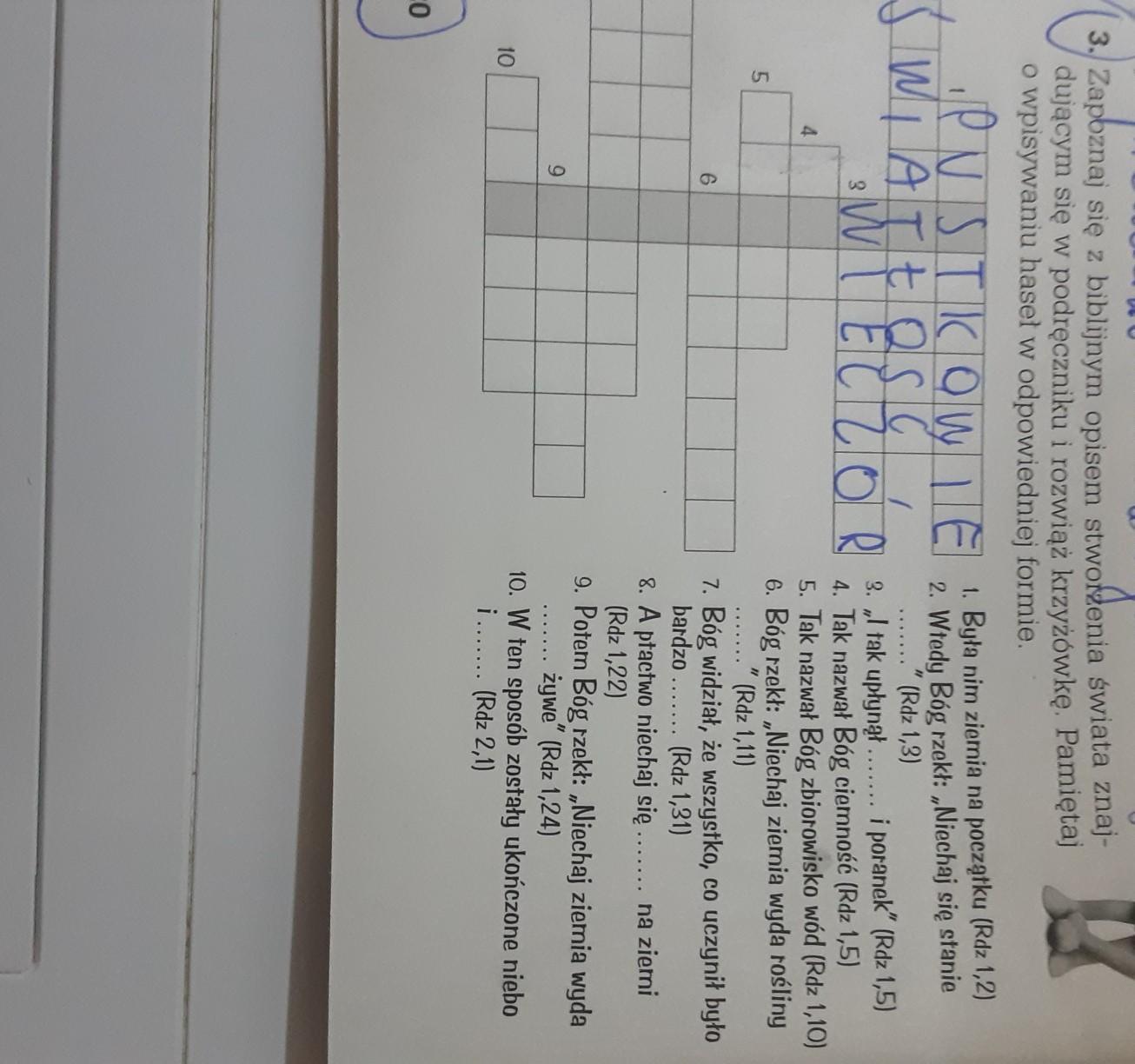
question img

Odpowiedzi 2

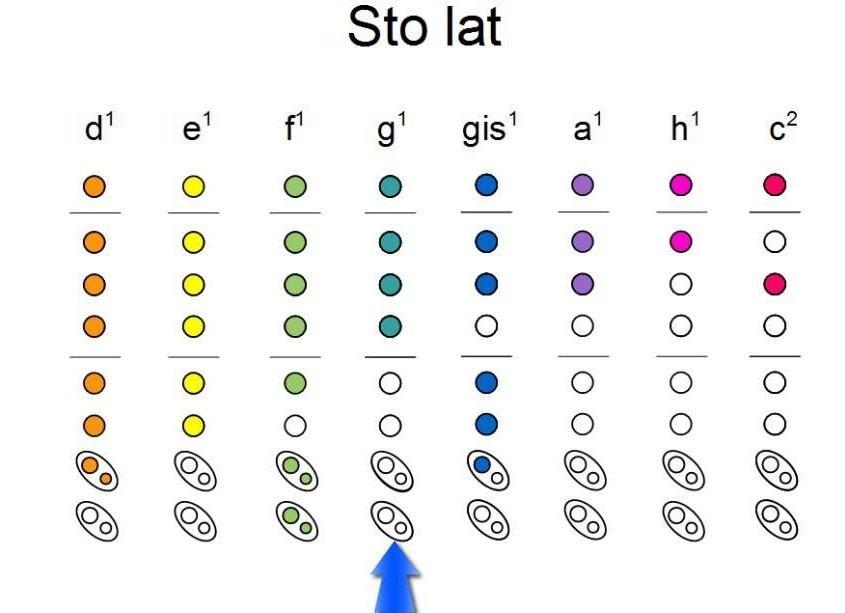
to są chwyty na flecie do piosenki STO LAT

Wyjaśnienie:

Mam nadzieję że trochę pomogłam

answer img

Odpowiedź:

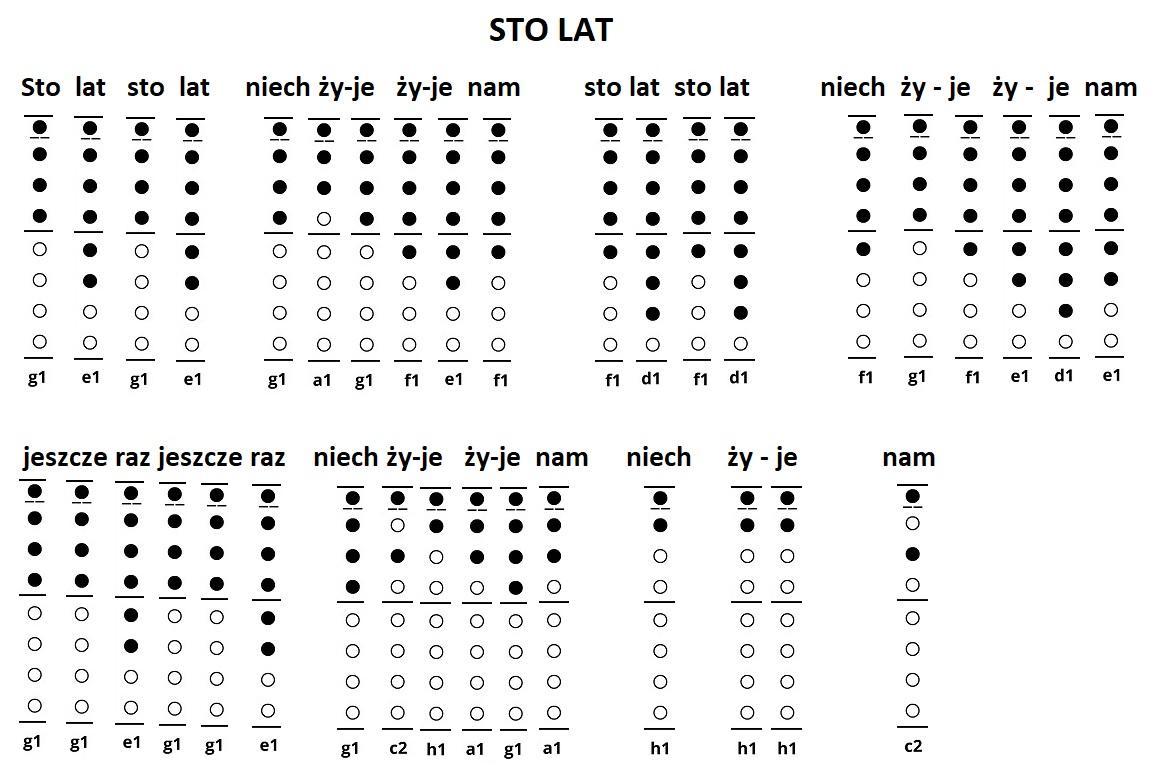
Sto lat - na flet

Wyjaśnienie:

w załączniku :)

answer img

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

pomocy z ta krzyżowa​
question img

1. pustkowie

2. światłość

3. wieczór

4. noc

5. morze

6. zielone

7. dobre

8. rozmnaża

9. istoty

10. ziemia

Hasło: STWORZENIE

W kręgach piersiowych są widoczne tzw. dołki żebrowe. Wyjaśnij ich rolę.
question img

Odpowiedź:

Dołki żebrowe mają za zadanie łączyć kręgi piersiowe z żebrami

Czy układ jest oznaczony, nieoznaczony czy sprzeczny?
question img
Jest oznaczony, ponieważ ma jedno rozwiązanie

Odpowiedź i szczegółowe wyjaśnienie:

[tex]\left \{ {{\dfrac{1-x}{2}-\dfrac{y+1}{3}=0\ /\cdot 6} \atop {\dfrac{2x-y}{4}+\dfrac{y-x}{2}=7\ /\cdot 4}} \right. \\\\\\\left \{ {{3(1-x)-2(y+1)=0} \atop {2x-y+2(y-x)=28}} \right. \\\\\left \{ {{3-3x-2y-2=0} \atop {2x-y+2y-2x=28}} \right. \\\\\left \{ {{-3x-2y+1=0} \atop {y=28}} \right. \\\\\left \{ {{-3x=2y-1} \atop {y=28}} \right. \\\\\\\left \{ {{-3x=2\cdot 28-1} \atop {y=28}} \right. \\\\\\\left \{ {{-3x=55\ /:(-3)} \atop {y=28}} \right. \\\\\\\left \{ {{x=\frac{55}{3}} \atop {y=28}} \right. \\[/tex]

Jak widzimy rozwiązaniem tego układu jest punkt (miejsce przecięcia się tych funkcji. Czyli ma jedno rozwiązanie, więc jest to układ OZNACZONY.

5 * Uzupełnij dialogi. Wpisz w każdą lukę brakujący fragment wypowiedzi, tak aby otrzymać spójne i logiczne teksty. 1 X: That's just not good enough. Y: again? X: I mean that you can do more to protect the environment. 2. X: Do you think this is good enough? Y: _ afraid X: OK, I'll try to do it better. Pliss na wczoraj ​
question img

Masz w załączniku mam nadzieję że pomogłem.

I jak coś to w podręczniku masz odpowiedź z dialogu.

answer img

Other Muzyka Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years