Ma ktoś pomysł na jeden refren do piosenki Szklanki, tekst na być parodią szkoły .

Odpowiedź:

Wydaje mi się że jest dobrze :))

Odpowiedź:

cena biletu normalnego --> a

cena biletu ulgowego --> a - 6

kwota zapłacona za 4 bilety normalne i 2 ulgowe --> 114 zł

4a + 2(a - 6) = 114

4a + 2a - 12 = 114

6a = 114 + 12

6a = 126

a= 126 : 6

a= 21

cena biletu normalnego --> 21 zł

cena biletu ulgowego --> 21 zł - 6 zł = 15 zł

Ile należy zapłacić za 3 bilety normalne i 1 bilet ulgowy?

3 * 21 zł + 15 zł = 63 zł + 15 zł = 78 zł

Odp. Za 3 bilety normalne i 1 bilet ulgowy należy zapłacić 78 zł.

Szczegółowe wyjaśnienie:

Odpowiedź:

1f

2c

3d

4h

5e

6b

7a

8g

Wyjaśnienie:

mam nadzieje że pomogłam<3

Odpowiedź:

a. Kolejność A,D,B,C

b. Dostępne światło - nasłonecznienie, Ilość pokarmu.

Wyjaśnienie:

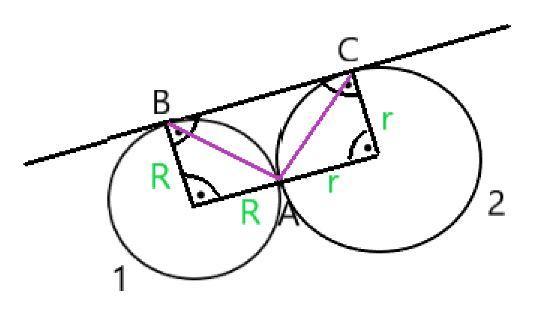
Dane:

Okręgi O1 i O2 są styczne zewnętrznie, zatem odległość pomiędzy nimi to suma ich promieni.

W tym zadaniu kluczowe jest wykonanie rysunku, na podstawie którego zauważymy potrzebne zależności. Wykonajmy go.

Styczną jest prosta, która ma tylko jeden punkt wspólny z okręgiem i jest prostopadła do promienia okręgu.

Wnioski?

1. Na podstawie rysunku zauważamy, że odcinki AB oraz AC są przeciwprostokątnymi trójkąt prostokątnych równoramiennych. Ramiona utworzone są z promieni każdego z okręgów.
2. Suma promieni okręgów jest jednocześnie szukaną odległością BC.

ROZWIĄZANIE

Aby obliczyć długość obu promieni, korzystamy ze wzoru na przeciwprostokątną w trójkącie 90, 45, 45 stopni.

Przeciwprostokątna to [tex]a\sqrt{2}[/tex], czyli tutaj [tex]r\sqrt{2}[/tex]

• Obliczamy długość promienia mniejszego okręgu - r.

[tex]r\sqrt{2} =4\sqrt{10} |:\sqrt{2}[/tex]

[tex]r=\frac{4\sqrt{10} }{\sqrt{2} } *\frac{\sqrt{2} }{\sqrt{2} }=\frac{4\sqrt{20} }{2}=\frac{2*2\sqrt{5} }{1} =4\sqrt{5}[/tex]

• Obliczmy teraz długość promienia drugiego okręgu - R.

[tex]R\sqrt{2} =12\sqrt{10} |:\sqrt{2}[/tex]

[tex]R=\frac{12\sqrt{10} }{\sqrt{2} } *\frac{\sqrt{2} }{\sqrt{2} } =\frac{12\sqrt{20} }{2} =6*2\sqrt{5} =12\sqrt{5}[/tex]

• Obliczamy długość odcinka BC, która jest sumą długość promieni.

[tex]r+R=4\sqrt{5} +12\sqrt{5} =16\sqrt{5}[/tex]

Odpowiedź:

Długość odcinka BC wynosi [tex]16\sqrt{5}[/tex]