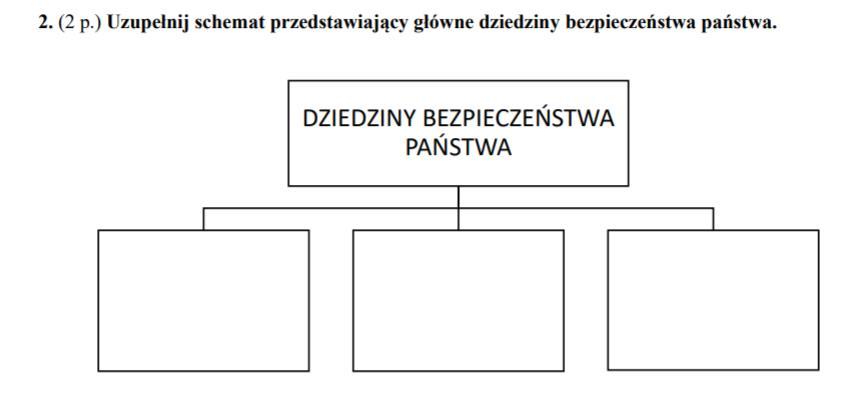
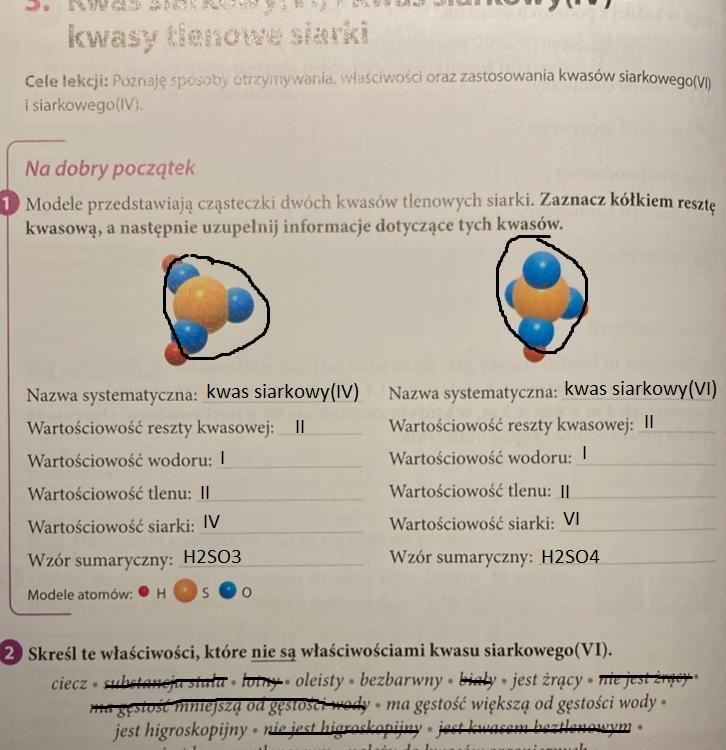
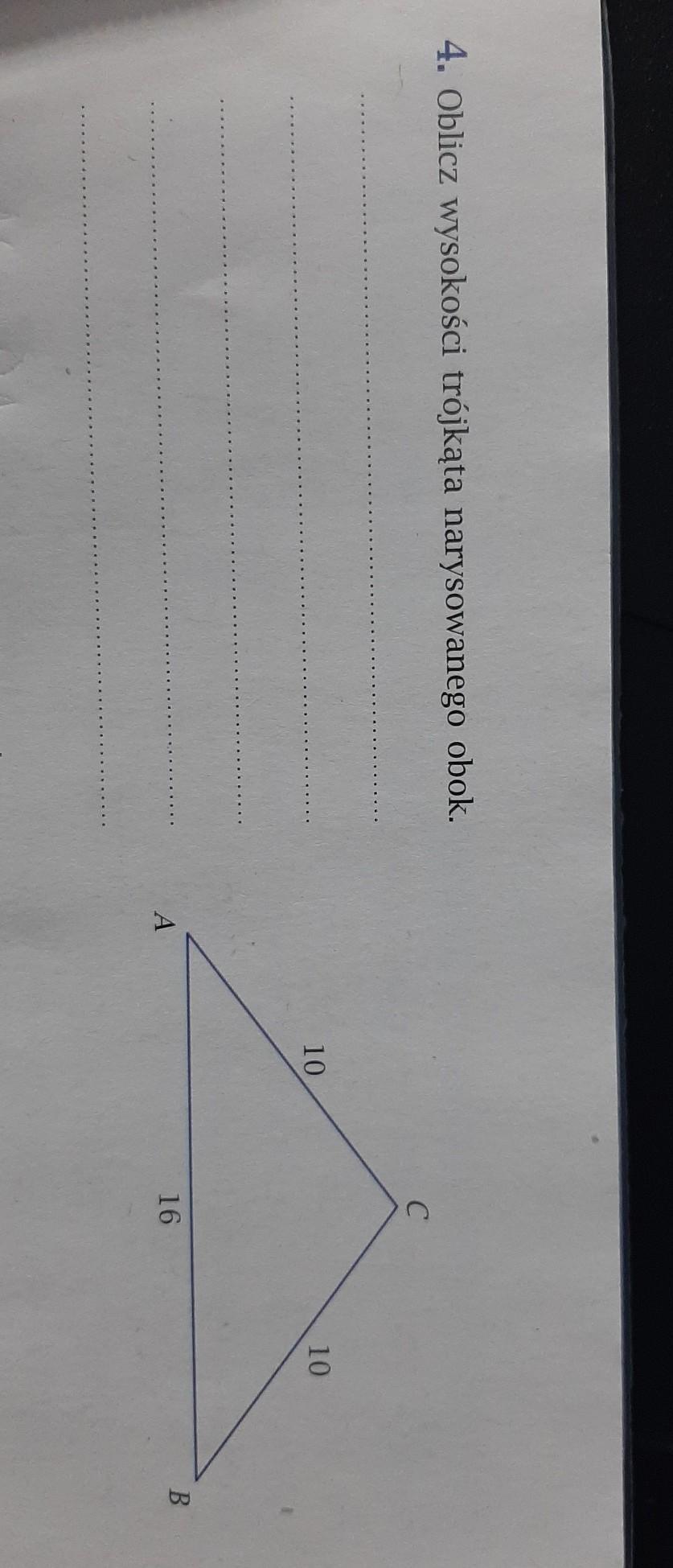
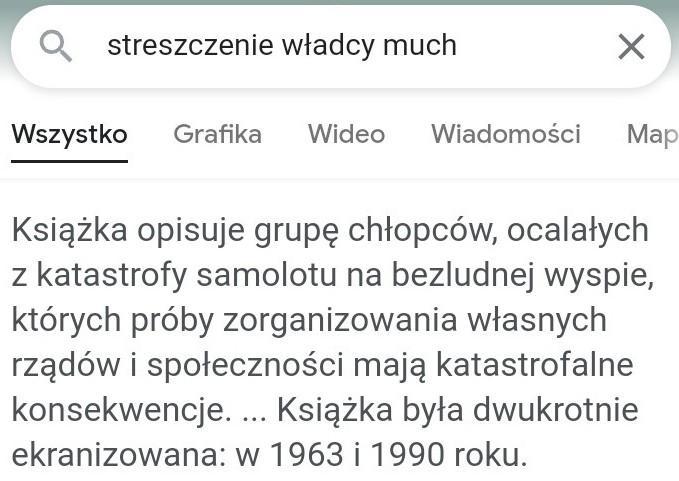
Ewa Winnicka Angole streszczenie Władcy much klasa 7

Odpowiedzi 1

Odpowiedź:

Odpowiedź gotową podałam na górze

answer img

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Uzupełnij schemat przedstawiający główne dziedziny bezpieczeństwa państwa.
question img

Odpowiedź:

Obrona Narodowa

Ochrona

Bezpieczeństwo społeczno-gospodarcze

Wyjaśnienie:

Modele przedstawiają cząsteczki dwóch kwasów tlenowych siarki. Zaznacz kółkiem resztę kwasową, a następnie uzupełnij informacje dotyczące tych kwasów. Nazwa systematyczna: Wartościowość reszty kwasowej: Nazwa systematyczna: Wartościowość reszty kwasowej: Wartościowość wodoru: Wartościowość wodoru: Wartościowość tlenu: Wartościowość tlenu: Wartościowość siarki: Wartościowość siarki: Wzór sumaryczny: Wzór sumaryczny: Modele atomów: H S O
question img

Zadanie w załączniku

answer img
Napisz którego urzędu w republice rzymskiej dotyczy każdy z opisów// Z historii plz na jutroo, zadanie w załączniku ​
question img

Odpowiedź:

1- konsulowie

2- trybuni ludowi

3- dyktator

Wyjaśnienie:

oblicz wyskokość trójkąta narysowanego obok​
question img

Odpowiedź i szczegółowe wyjaśnienie:

Wysokość tego trójkąta obliczymy wykorzystując Twierdzenie Pitagorasa.

Wysokość (h) z wierzchołka C przecina w połowie podstawę AB wynoszącą 16 i tworzy trójkąt prostokątny o przyprostokątnej 8, wysokości (h) i przeciwprostokątnej wynoszącej 10.

Zatem:

[tex]8^2+h^2=10^2\\\\h^2=10^2-8^2\\\\h^2=100-64\\\\h^2=36\\\\h=\sqrt{36}\\\\h=6[/tex]

Odpowiedź: wysokość tego trójkąta ma miarę 6 jednostek.

Other Polski Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years