2. Jak - Twoim zdaniem - można się stać osobą niezależną? ​

Odpowiedź:

Zadanie wykonam w załączniku

Środek odcinka AB jest odległy od początku układu współrzędnych o  2.5.

Szczegółowe wyjaśnienie:

Witaj :)

1. My grandma goes to church every Sunday.

2. Should I brush my teeth after lunch?

3. Derek cannot take the rubbish out now because he is sleeping.

4. We have to leave the house in five minutes or we'll be late.

5. According to the school rules, girls mustn't wear make-up.

6. Do your parents use social networks?

7. What are you doing? Do you have a minute?

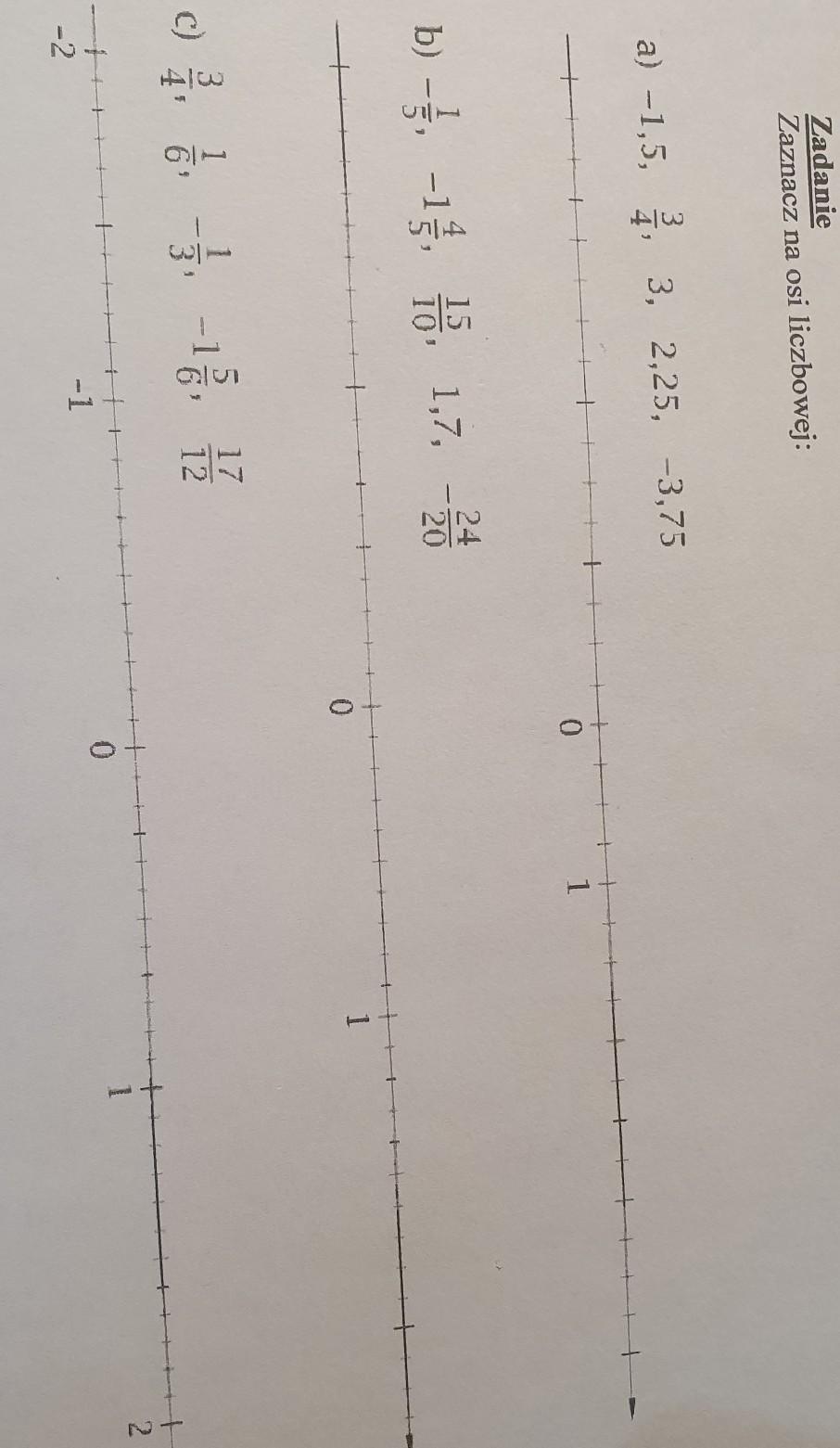
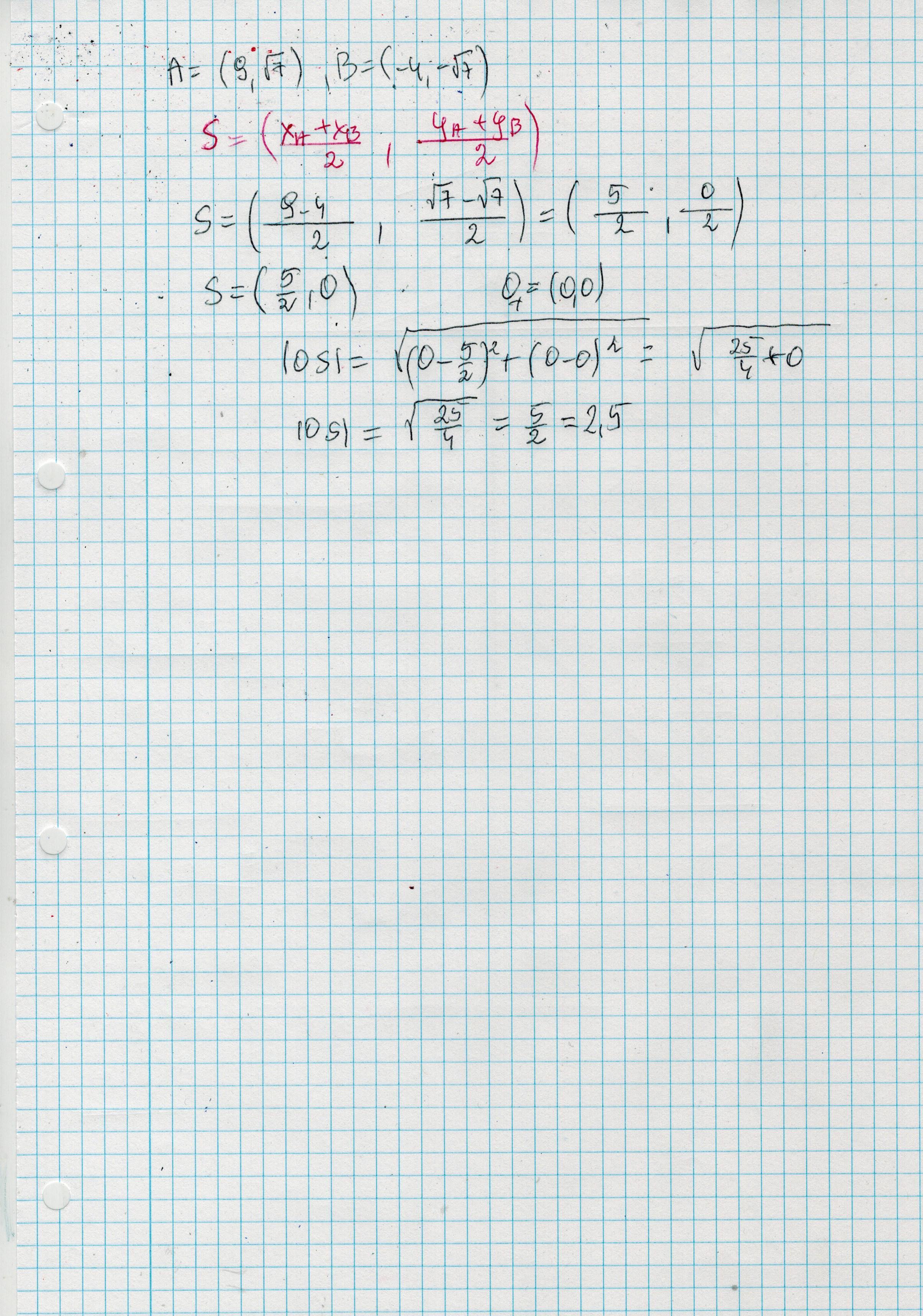Wykonując tego typu zadania można myśleć o osi jak o linijce. Na początku dla ułatwienia zadania zaznacz sobie na niej wszystkie liczby całkowite (czyli te bez ułamków).  Patrz 1 załącznik

Potem sprawdzamy dokładność "linijki", czyli co ile "kresek" jest liczba całkowita. W pod punkcie a co 4 kreski jest liczba całkowita, więc każda kreska odpowiada [tex]\frac{1}{4}[/tex] czyli [tex]0.25[/tex]. Teraz aby zaznaczyć np. 2.25 szukamy [tex]2[/tex], a potem najbliższej kreski do liczby po przecinku. W tym przypadku to 1 kreska, czyli idealnie [tex]2.25[/tex] (lepiej zawsze brać liczby bliższe 0 na osi liczbowej), zaznaczamy 2.25. Kiedy liczba nie będzie się pokrywać z najbliższą kreską, zaznaczamy gdzie mniej więcej powinna być.

W przypadku liczb ujemnych (mniejszych od 0, przed nim) robimy to samo, tylko kiedy znajdziemy najbliższą kreskę od strony 0, to musimy pamiętać, że musimy przesunąć tym razem w lewo, a nie w prawo.

Liczę, że dobrze wytłumaczyłem (przypominam o wybraniu najlepszej odpowiedzi)

Odpowiedź:

Szyfr

ż = n, -zamieniamy ''ż na n'' np. Pewża-Pewna

f =m,- zamieniamy'' f na m'' np. fała- mała