czy patriarchalna postawa telemacha (uzasadniająca dominującą rolę mężczyzny w życiu społecznym i rodzinnym) byłaby uznana za wartościowa we współczesnym świecie Uzasadnij swoje zdanie na ten temat fragment Odyseja​

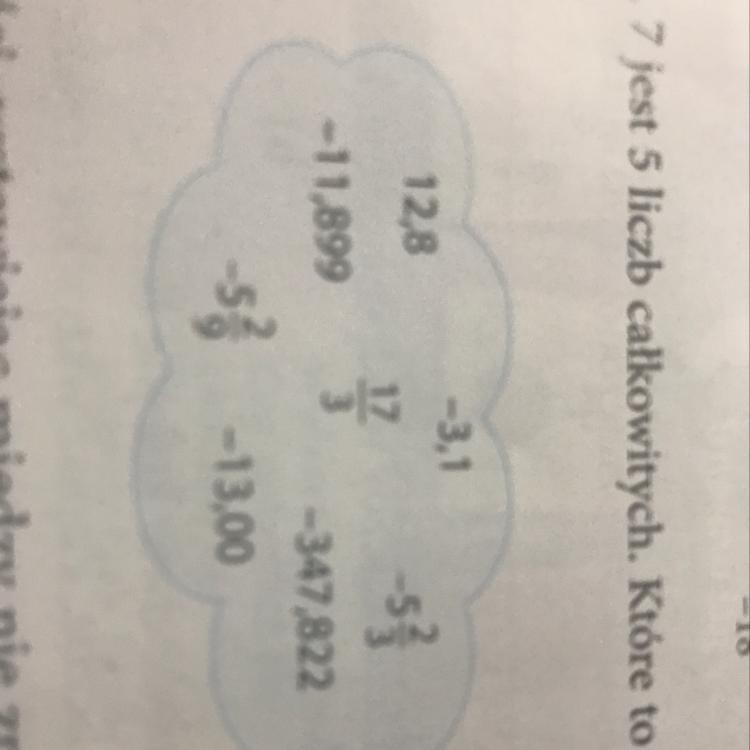
12,8 < 13-11,899 > -12-3,1 < -3

[tex]5\frac{2}{3} < 6[/tex]

 [tex]-5\frac{2}{9} < -5[/tex]

[tex]-5\frac{2}{3} > -6[/tex]  

-348 < -347,822

-13 = -13

Liczby całkowite to liczby naturalne {1,2,3,4..}  i liczby do nich przeciwne {-1,-2,-3,-4..}  oraz liczba zero.Liczba całkowita nie może mieć części ułamkowej ani liczb po przecinku.

Znaki <, > i =

• a < b → liczba a jest mniejsza od b
• a > b → liczba a jest większa od b
• a = b → liczby a i b są równe

Rozwiązanie

• 12,8

Liczby całkowite, które znajdują się koło 12,8 to liczba 12 oraz 13. Rozważmy obydwie liczby, aby znaleźć najbliższą.  W tym celu możemy policzyć różnice pomiędzy nimi.

12,8 - 12 = 0,8

Odległość pomiędzy liczą 12,8 a liczbą 12 wynosi 0,8.

13 - 12,8 = 0,2

Odległość pomiędzy liczą 12,8 a liczbą 13 wynosi 0,2.

Z tego wynika, że najbliższą liczbą całkowitą dla liczby 12,8 jest 13.

12,8 to liczba mniejsza od 13, zapis tego wygląda następująco:

Wniosek: 12,8 < 13

• -11,899

Wraz z rosnącą odległością od 0, liczby ujemne są coraz mniejsze.

Najbliższa liczba całkowita dla -11,899 to -12.

Liczba -12 znajduje się dalej od zera niż -11,899, dlatego jest mniejsza:

Wniosek: -11,899 > -12

• -3,1

Najbliższa liczba całkowita dla -3,1 to -3.

Liczba -3,1 znajduje się dalej od zera niż -3, dlatego jest od niej mniejsza:

Wniosek: -3,1 < -3

• [tex]\frac{17}{3}[/tex]

W pierwszej kolejności należy wyłączyć całość z ułamka niewłaściwego.

[tex]\frac{17}{3} = 5\frac{2}{3}[/tex]

[tex]\frac{2}{3}[/tex] to ułamek większy niż [tex]\frac{1}{2}[/tex], czyli większy niż połowa, dlatego [tex]5\frac{2}{3}[/tex] jest bliżej liczby 6 niż liczby 5.

Wniosek: [tex]5\frac{2}{3} < 6[/tex]

• [tex]-5\frac{2}{9}[/tex]

[tex]\frac{2}{9}[/tex] to ułamek mniejszy  niż [tex]\frac{1}{2}[/tex], czyli mniejszy niż połowa, dlatego  [tex]-5\frac{2}{9}[/tex] jest bliżej -5 niż liczby -6.

Liczba  [tex]-5\frac{2}{9}[/tex] znajduje się dalej od zera niż -5, więc jest mniejsza od niej.

Wniosek:  [tex]-5\frac{2}{9} < -5[/tex]

• [tex]-5\frac{2}{3}[/tex]

[tex]\frac{2}{3}[/tex] to ułamek większy niż [tex]\frac{1}{2}[/tex], czyli większy niż połowa, dlatego [tex]-5\frac{2}{3}[/tex] znajduje się bliżej liczby -6 niż liczby -5.

Liczba [tex]-5\frac{2}{3}[/tex] jest bliżej zera niż -6, dlatego jest większa od liczby -6.

Wniosek:[tex]-5\frac{2}{3} > -6[/tex]  

• -347,822

Liczba -347,822 znajduje się pomiędzy liczbą -348 a liczbą -347.

Część po przecinku jest większa niż pół, czyli znajduje się bliżej liczby -348.

Liczba -348 jest mniejsza od -347,822, ponieważ znajduje się dalej od zera.

Wniosek: -348 < -347,822

• -13,00

Liczba -13 to liczba całkowita, dlatego używamy znaku równości:

Wniosek: -13 = -13

bym pomogła ale nie wiem jak to zrobić hshs

Witaj :)

1. How much pocket money do you get?

2. Go to the chemist to buy some bandages.

3. I like fried chicken the most.

4. I'm allergic to dairy products.

5. The knives are already on the table.

6. Where are the changing rooms?

7. What are you ordering for dessert?

Odpowiedź:

1.naskórek

2.skóra właściwa

3.tkanka podskórn

1 naskórek- jest zewnętrzną warstwą skóry która chroni nasz organizm przed światem zewnętrznym

2. skóra właściwa to środkowa warstwa skóra składa się z licznych włókien kolagenowych znajdują się w niej naczynia krwionośne i zakończenia nerwowe i gruczoły

3. tkanki podskórne najgłębiej położona warstwa z tkanki tłuszczowej chroni przed urazami izolacja ciepła i kształtowanie powierzchni ciała

Wyjaśnienie:

chyba pomogłem