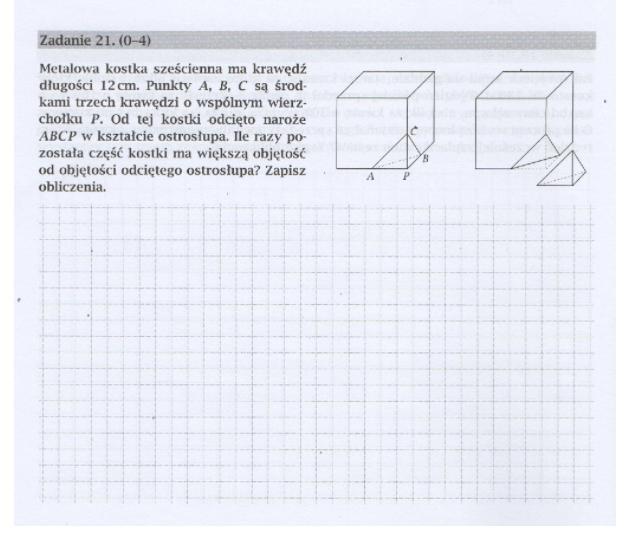
Najpierw obliczamy objętość sześcianu :)Wzór na objętość sześcianu:
[tex]V=a^3~~czyli~~a*a*a[/tex]
gdzie:
[tex]V=objetosc\\a=krawedz[/tex]
Wstawiamy do wzoru:
[tex]V=a^3\\V=12cm^3\\V=12cm*12cm*12cm\\V= 144cm*12cm\\\underline{V=1728cm^3}[/tex]
Wiemy już jaką objętość ma sześcian, więc możemy przystąpić teraz do obliczenia objętości ostrosłupa ze wzoru:
[tex]V=\frac{1}{3} Pp*H[/tex]
gdzie:
[tex]V=objetosc\\Pp=Pole~~podstawy\\H=wysokosc[/tex]
Aby obliczyć objętość ostrosłupa, musimy obliczyć najpierw pole podstawy, aby móc doliczyć się wyniku :).
Korzystamy ze wzoru na pole trójkąta:
[tex]\frac{a*h}{2}[/tex]
Wstawiamy do wzoru:
[tex]P=\frac{a*h}{2} \\P=\frac{6cm*6cm}{2} \\P=\frac{36cm}{2} \\P=18cm^2[/tex]
Mamy już to co potrzebowaliśmy, dlatego możemy już obliczyć objętość ostrosłupa:
[tex]V=\frac{1}{3} Pp*H\\\\V=\frac{1}{3} *18cm^2*6cm\\\\V=\frac{1}{\not{3}~^1} *\frac{\not{18}~^6}{1} *6\\\\V=\frac{6}{1} *6\\\\V=6cm^2*6cm\\\\\underline{V=36cm^3}[/tex]
Obliczyliśmy objętości dwóch brył, więc możemy przejść do dalszej części zadania, która brzmi: ,,(...) Ile razy pozostała część kostki ma większą objętość od objętości odciętego ostrosłupa?"
Czyli najpierw obliczymy sobie jaką objętość ma pozostała część kostki odejmując od objętości sześcianu, objętość ostrosłupa:
[tex]V_{pozostalej~~czesci~~szescianu} =V_{szescianu} -V_{ostroslupa} \\V_{pozostalej~~czesci~~szescianu}=1728cm^3-36cm^3\\\underline{V_{pozostalej~~czesci~~szescianu}=1692cm^3}[/tex]
Mamy już objętość pozostałości sześcianu, więc możemy teraz obliczyć ile razy pozostała część kostki ma większą objętość od objętości odciętego ostrosłupa dzieląc objętość pozostałości sześcianu przez objętość ostrosłupa:
[tex]\frac{1692cm^3}{36cm^3} =\boxed{47cm^3}[/tex]
[tex]\boxed{Odp: Pozostala~~czesc~~kostki~~jest~~o~~47cm^3~~razy~~wieksza~~od~~odcietego~~rogu.}[/tex]