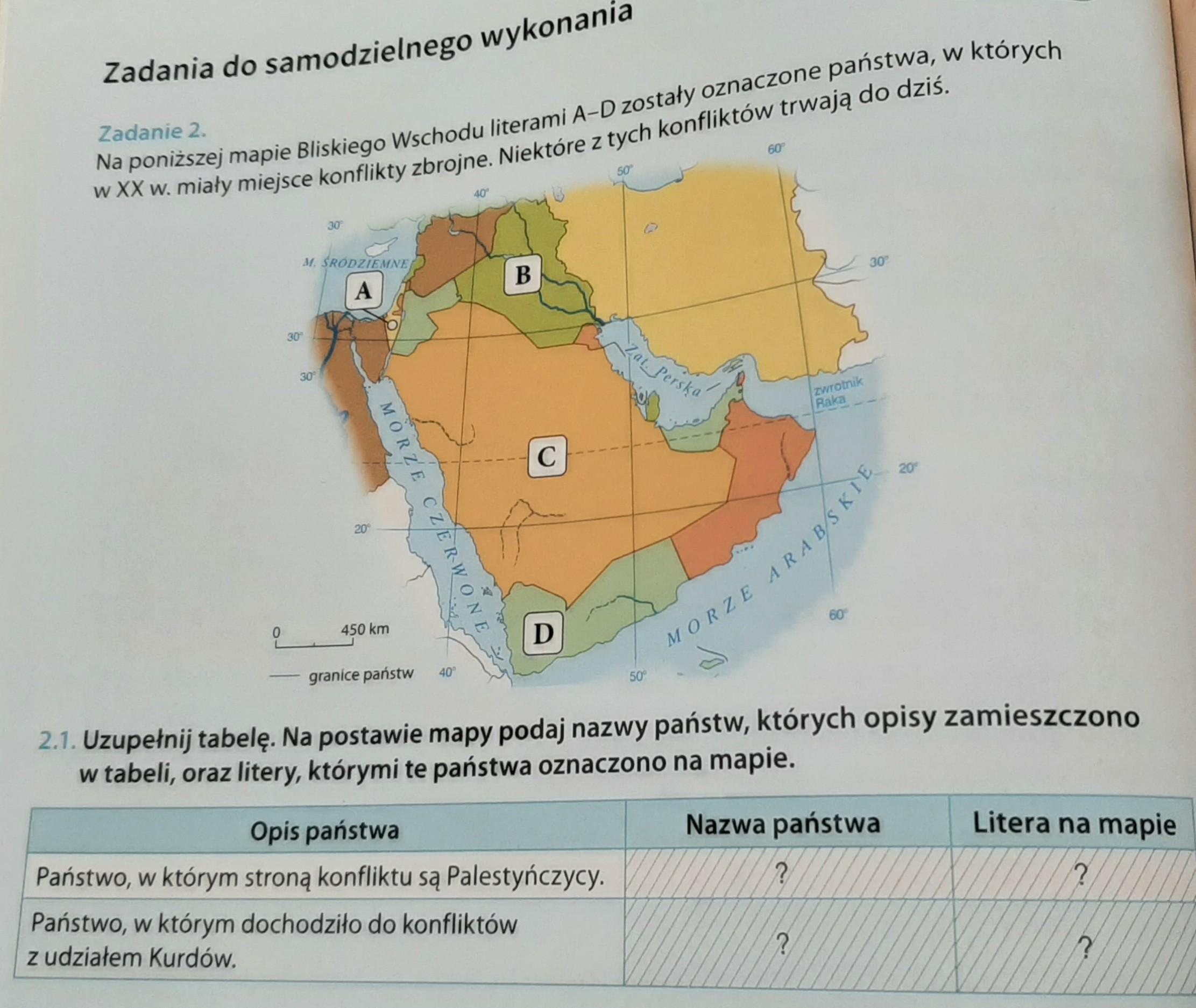
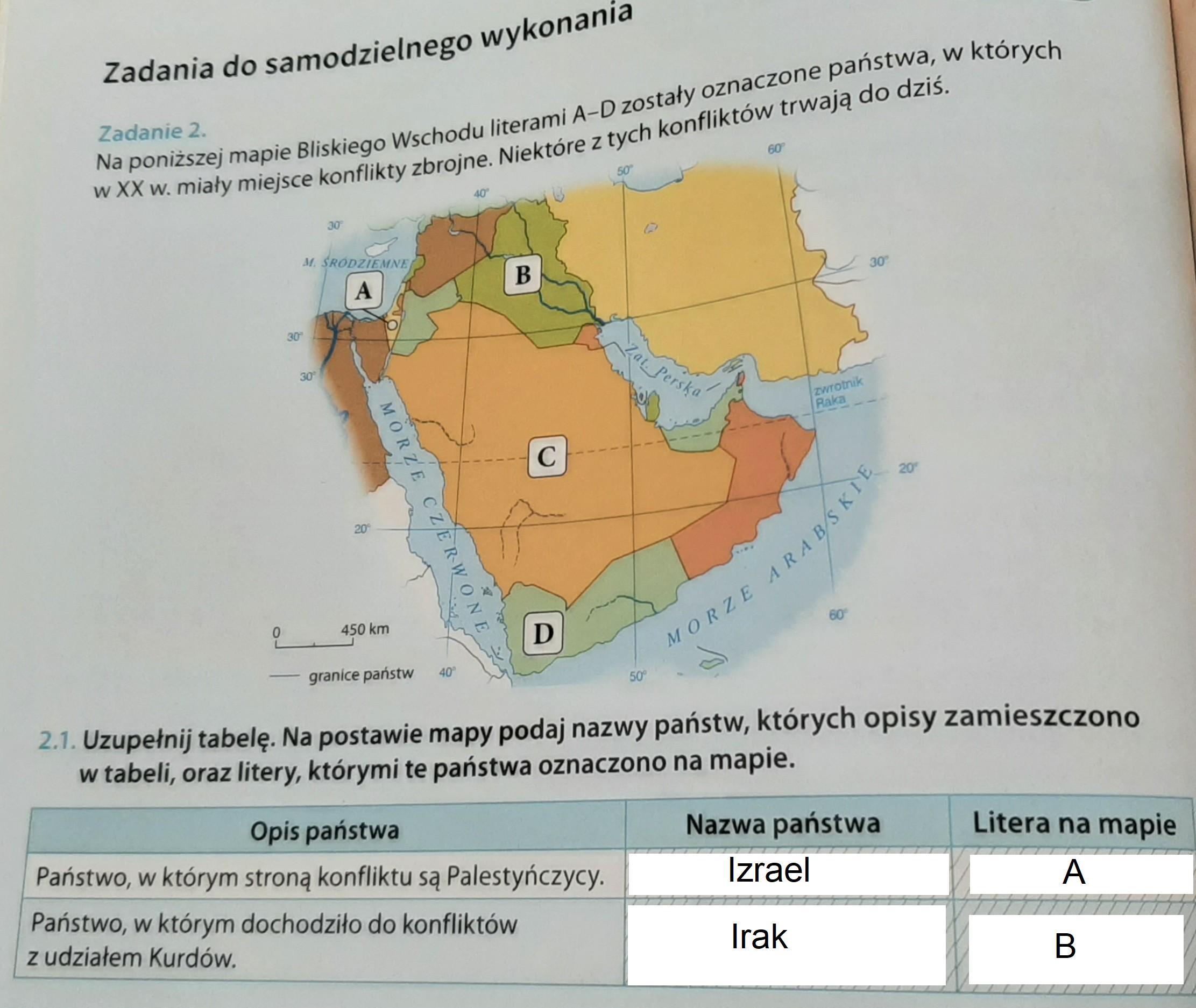
W gospodarce każdego państwa rynek pelni wiele funkcji. Dopisz do podanych opisów nazwy funkcji rynku. ​

question img

Odpowiedzi 1

Odpowiedź:

A. -  funkcja akceptacji towarów i usług

B. - funkcja równowagi

C. - funkcja informacyjna

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

7 Przeczytaj trzy teksty związane z nauką i techniką. Która z podanych opcji A-C jest poprawna? 8 Underwater forest Several years ago, scuba diver Chas Broughton discovered an underwater forest of massive ancient cypress trees. Located twenty kilometres from the coast of Alabama, in the Gulf of Mexico, it is home for thousands of sea animals. Chas told a local journalist about the discovery, but they kept it secret until 2004, when Hurricane Ivan uncovered some of the trees. Then scientists started exploring the area. They have suggested that the forest is more than 50,000 years old. In the past, the ocean level in the area was 125 metres lower than today, but when it rose, the water swallowed the trees up. The forest is so unique that conservationists are now working to make it a marine protected area. 1 The scientists A found out about the discovery from a local journalist. B started visiting the area after the 2004 hurricane. C are trying to protect the forest.​

B: Started visiting the area after the 2004 hurricane

5 Read the Look out! box. Choose the correct words to complete the sentences. 1 I travelled /I've travelled to Paris on the Eurostar last May 2 Tom loves the Hunger Games books. He read / He's read them all. 3 'Did you ever eat / Have you ever eaten at the Chinese restaurant in town?' 'No, never.' 4 I bought / I've bought this scarf on Saturday. Do you like it 5 'New York is an amazing city.' 'I know. I went / I've been there several times.' 6 Amy was at a music festival last weekend. Unfortunately, she lost / she's lost her phone there. 2​
question img

Odpowiedź:

1. I've travelled

2. He's read

3. Have you ever eaten

4. I bought

5. I've been

6. She's lost

PROSZĘ O POMOCZad.2 Na poniższej mapie Bliskiego Wschodu literami A-D zostały oznaczone państwa, w których w XX wieku miały miejsce konflikty zbrojne. Niektóre z konfliktów trwają do dziś.​
question img

Odpowiedź:

Wyjaśnienie:

answer img
Pole trapezu równoramiennego o wysokości 5 jest równe 45. Odcinek łączący środki ramion tego trapezu ma długość ........ pls pomocy

W zadaniu należy obliczyć, ile wynosi odcinek łączący środki ramion trapezu równoramiennego o wysokości 5 i polu równym 45.

Odcinek łączący środki ramion trapezu równoramiennego wynosi 9.

Oznaczenia:

x - odcinek łączący środki ramion trapezu równoramiennego (szukana w zadaniu)

Rysunek pomocniczy w załączniku.

Z własności trapezu równoramiennego wynika, że:

[tex]x = \cfrac{a+b}{2}[/tex]

Dane z zadania:

[tex]h = 5 \\\\P = 45[/tex]

Przypomnijmy wzór na pole trapezu:

[tex]P = \cfrac{(a+b)\cdot h}{2}[/tex]

gdzie:

a, b - długości podstaw trapezu

h - wysokość trapezu

Przekształcamy równanie:

[tex]x = \cfrac{a+b}{2}\ | \cdot 2 \\\\a+b = 2x[/tex]

Podstawiamy tą zależność do wzoru na pole trapezu i otrzymujemy:

[tex]\cfrac{2x \cdot 5}{2} = 45[/tex]

Wyznaczamy x - szukana w zadaniu:

[tex]5x = 45\ | : 5 \\\\\boxed{x = 9}[/tex]

Wniosek: Odcinek łączący środki ramion trapezu równoramiennego wynosi 9.

#SPJ2

answer img

Other Przedsiębiorczość Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years