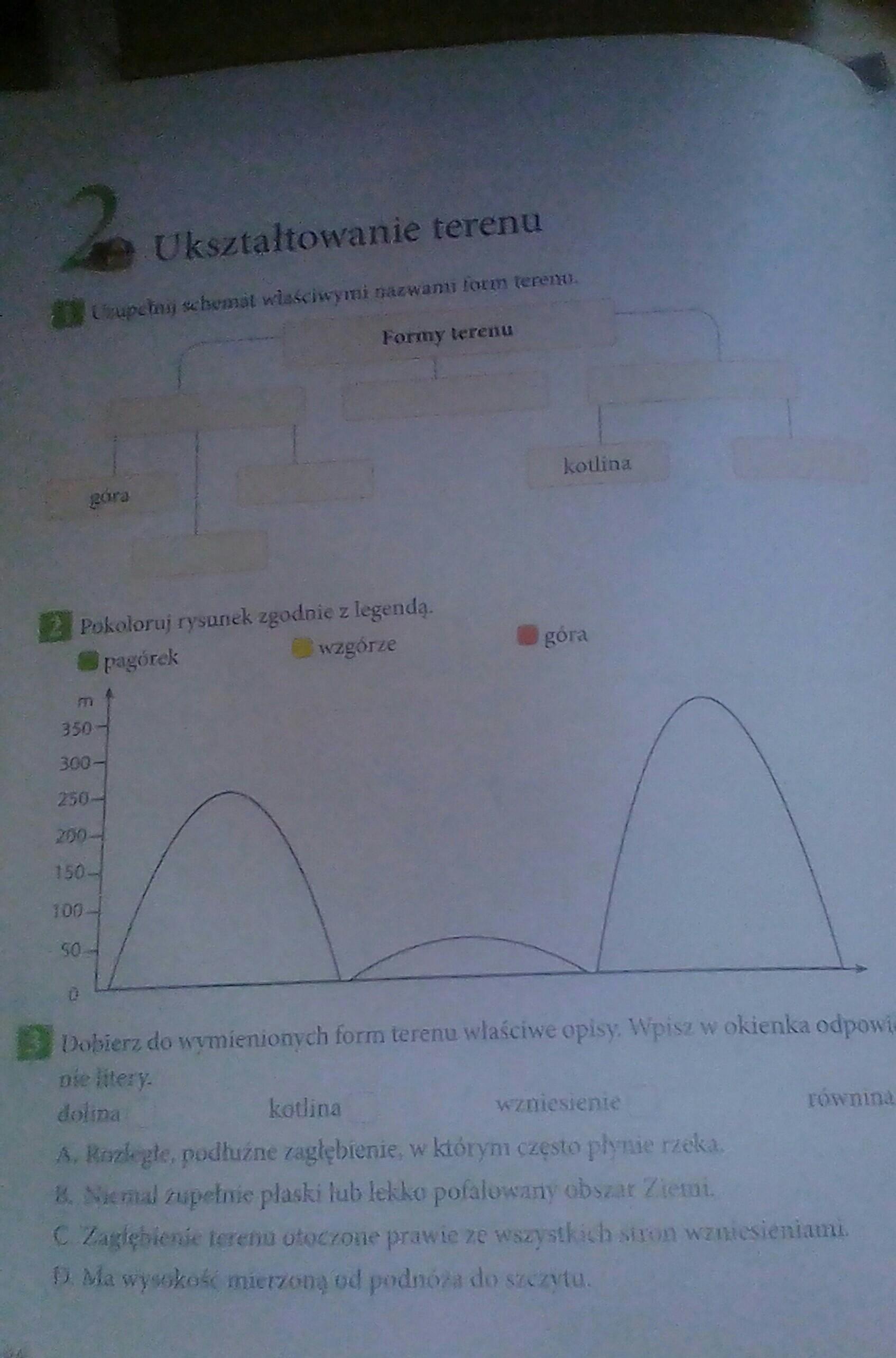
Zad 1 Uzupełnij schemat właściwymi nazwami form terenu. Zad 2 Pokoloruj rysunek zgodnie z legendą. Zad 3 Dobierz do wymienionych form właściwe opisy wpisz w okienka odpowiedni litery​

Odpowiedź:

1-mniej w soku owocowym

2-mniej w maśle

3-mniej w jogurcie naturalnym ;)

To wszystko ;)

Wyjaśnienie:Mam nadzieję że pomogłam

Kanada,Nowa Zelandia,.......

Odpowiedź:

kanada i nowa Zelandia

Oznaczmy:

a,b - długość krawędzi podstawy prostopadłościanu

H - wysokość prostopadłościanu

d1=√15m

d2=2√10m

d3=3√5m

d1,d2,d3 - długości przekątnych ścian prostopadłościanu

d1=√(a²+b²)

√(a²+b²)=√15m|²

a²+b²=15m²

d2=√(a²+H²)

√(a²+H²)=2√10m|²

a²+H²=40m²

d3=√(b²+H²)

√(b²+H²)=3√5m|²

b²+H²=45m

Otrzymaliśmy układ 3 równań z trzema niewiadomymi:

a²+b²=15m²

a²+H²=40m²   ⇔   H²=40m²-a²

b²+H²=45m²

b²+40m²-a²=45m²

b²-a²=45m²-40m²

-a²+b²=5m²

a²+b²=15m²

--------------

2b²=20m²|:2

b²=10m²

b=√10 m

a²+b²=15m²

a²+10m²=15m²

a²=15m²-10m²

a²=5m²

a=√5 m

H²=40m²-a²

H²=40m²-5m²

H²=35m²

H=√35 m

Obliczymy objętość prostopadłościanu:

V=abH

V=√5 m·√10 m·√35 m

V=√5·√5·√2·√35 m³

V=5√70 m³

fgfgddgddf