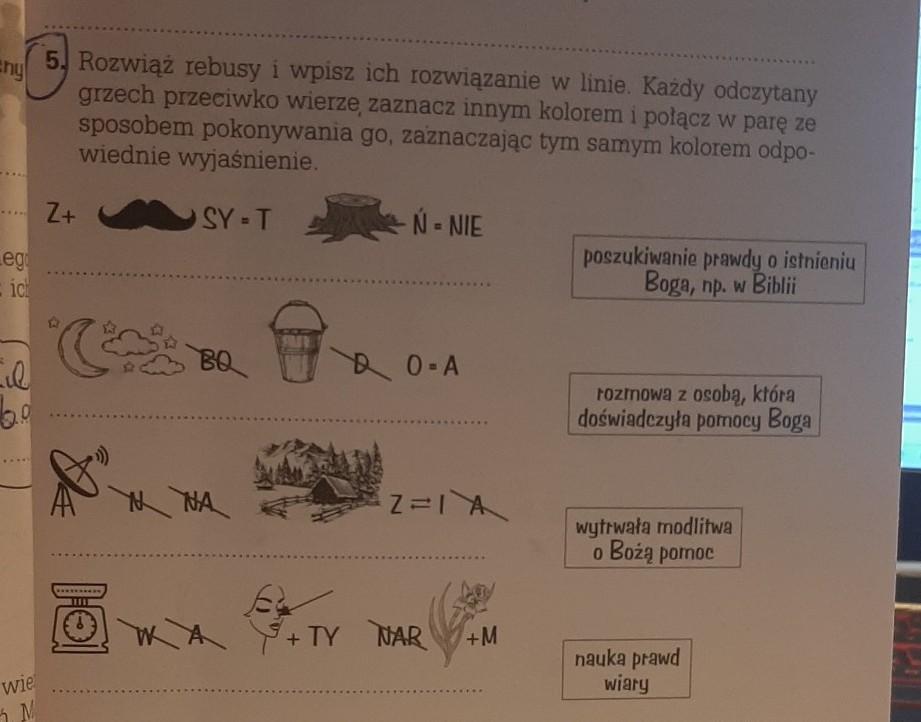
Rozwiąż rebusy Wpisz ich rozwiązania w linii każdy odczytane grzechy przeciwko wierze Zaznacz innym kolorem i Połącz w pary ze sposobem wykonywania go zaznaczając tym samym kolorem odpowiednie wyjaśnienia klasa 5 zadanie 5 strona 33 religiadaje pięć gwiazdek plis​

Odpowiedź:

Patrycjusze − uprzywilejowana, wyższa warstwa społeczna, która pojawiła się w okresie królestwa oraz republiki w starożytnym Rzymie. Posiadali pełne prawa polityczne oraz wyłączność obejmowania urzędów.                     Plabejusz - wolny obywatel rzymski, który przysługujące mu prawa nabył dopiero w okresie republiki. Plebejusze tworzyli podstawę rzymskiej armii, w której służyli jako ciężkozbrojna piechota. Odgrywali ważną rolę w społeczeństwie antycznego Rzymu

Wyjaśnienie:

Odpowiedź i szczegółowe wyjaśnienie:

[tex]1.\\f(x)=-3x^2+6x-3\\\\a=-3;\ b=6;\ c=-3\\\Delta=b^2-4ac\\\Delta=6^2-4\cdot(-3)\cdot(-3)=36-36=0[/tex]

[tex]2.\\f(x)=a(x-3)^2+5\\f(x)=a(x^2-6x+9)+5\\f(x)=ax^2-6ax+9a+5\\\\\Delta=-10\\\Delta=b^2-4ac\\\\a=a;\ b=-6a;\ c=9a+5\\\\(-6a)^2-4\cdot a\cdot(9a+5)=-10\\36a^2-36a^2-20a=-10\\-20a=-10\\a=\frac12[/tex]

Obliczymy teraz punkt przecięcia się wykresu funkcji z osią OY. Punkt ten obliczymy w ten sposób, że współrzędna x-owa jest równa 0. Zatem:

[tex]f(x)=\frac12(x-3)^2+5\\f(0)=\frac12(0-3)^2+5\\f(0)=\frac12\cdot(-3)^2+5\\f(0)=\frac12\cdot9+5\\f(0)=\frac92+5\\f(0)=\frac92+\frac{10}{2}\\f(0)=\frac{19}{2}\\f(0)=9\frac12[/tex]

W załączeniu wykres funkcji dla zadania 2.

Odpowiedź:

Lepiej zastosować równoważniki zdania, ponieważ będą one bardziej wyraźne.

Nie wolno tu wchodzić!  Zakaz wejścia

Prosimy o przechodzenie  drugą stroną ulicy.     Przejście drugą stroną ulicy.

Musisz uważać,  podłoga jest tu śliska.    Śliska podłoga

nie wiem jak zrobić pierwsze zdanie, przepraszam

Odpowiedź:

trzęsienia ziemi, ponieważ leży na styku trzech ...