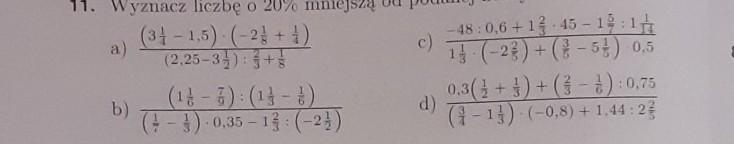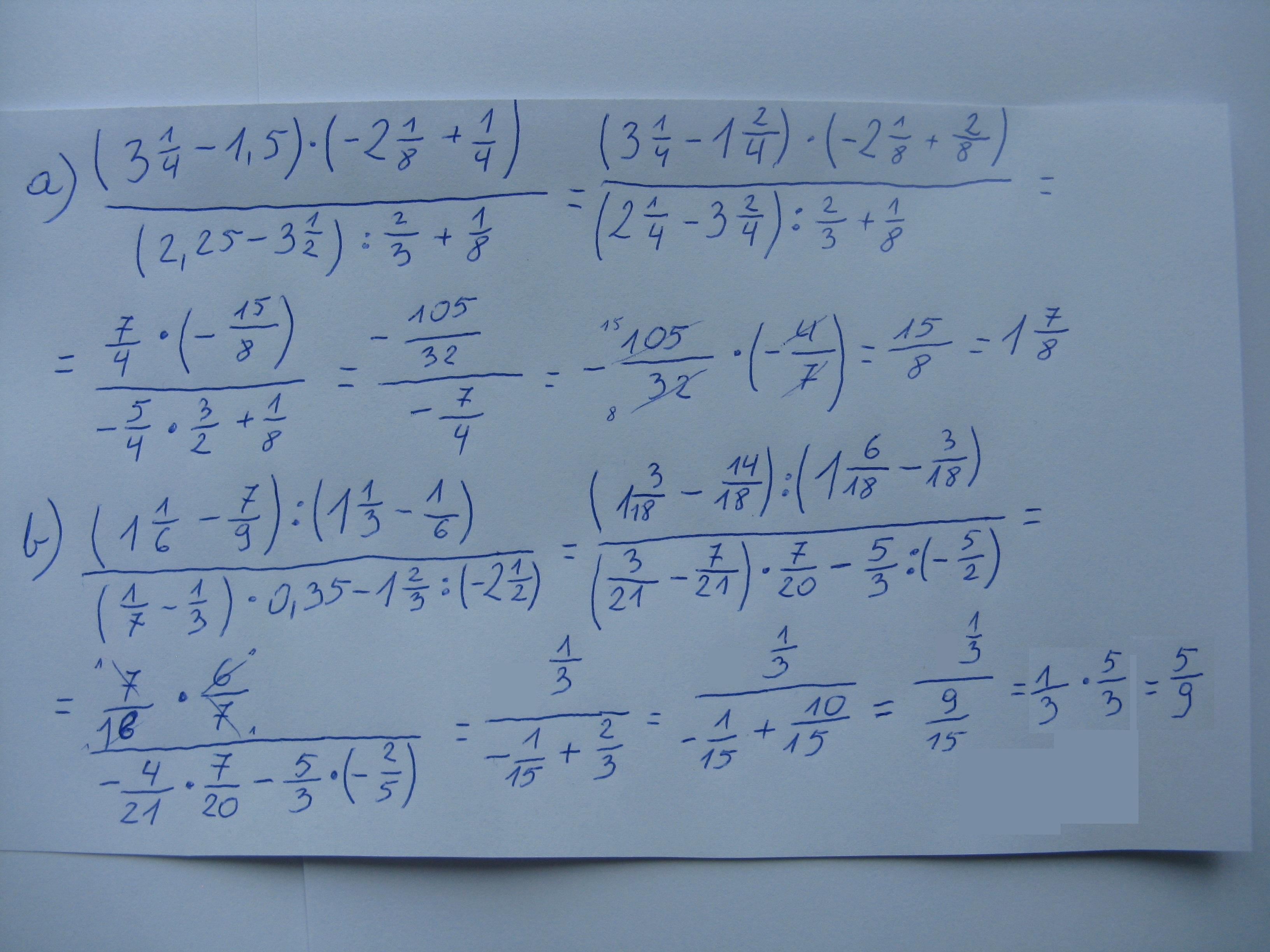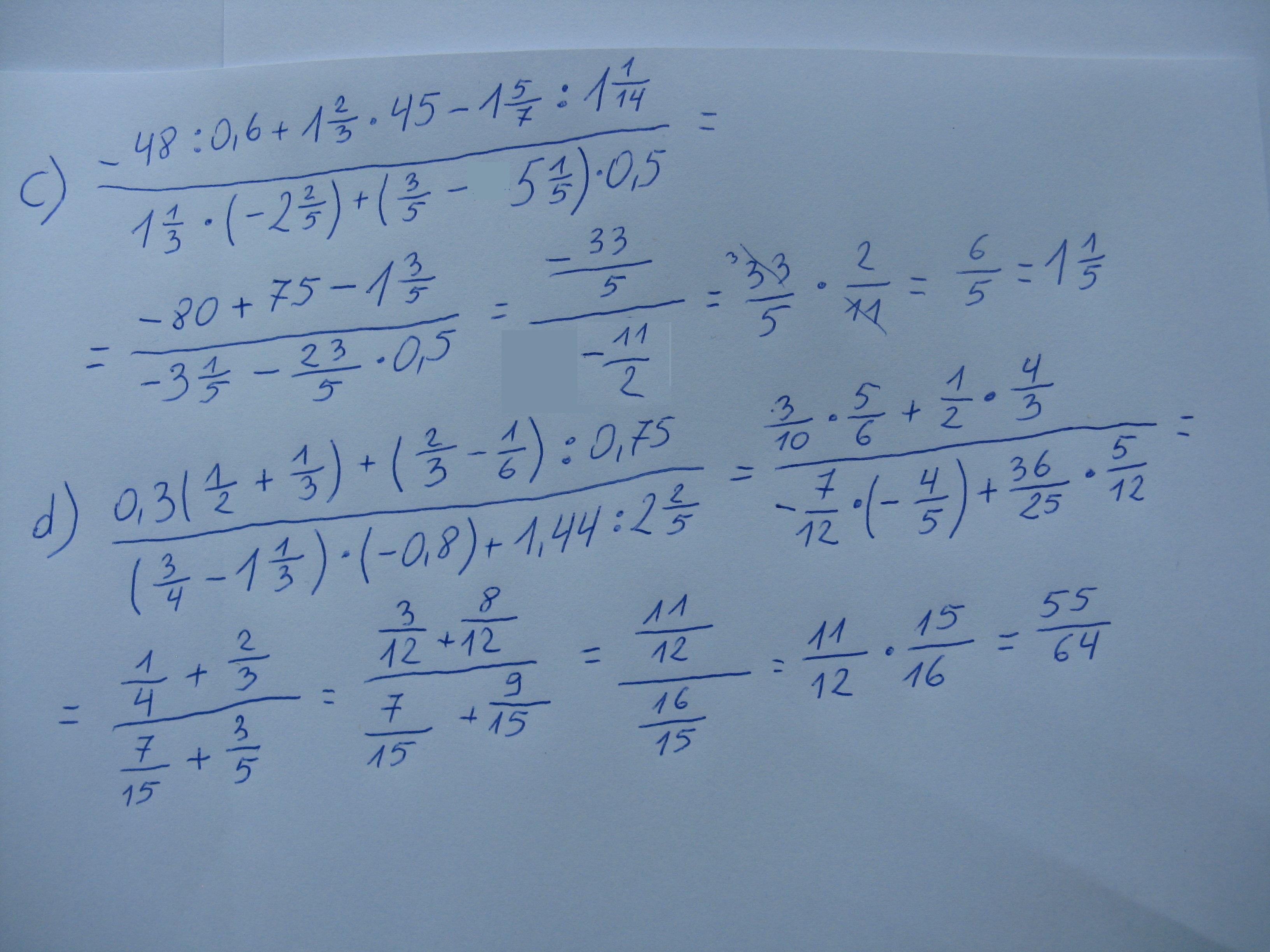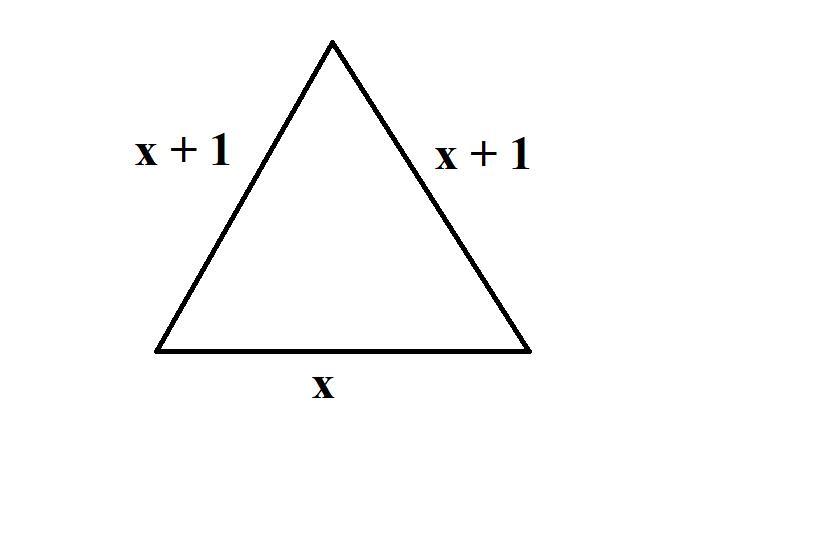Bóg w rózny sposób objawia się człowiekowi przeczytaj fragmenty Pisma Świętego: Rz 1,20a Rz 2,14-15 i Hbr 1,1-2a i wypisz słowa klucze będące Bożego Objawienia - D____a B__e, S______e, P_____y i J___s C______s

Odpowiedź:

a)  [tex]1\frac{1}{2}[/tex]

b)  [tex]\frac{4}{9}[/tex]

c)  [tex]\frac{24}{25}[/tex]

d)  [tex]\frac{11}{16}[/tex]

Szczegółowe wyjaśnienie:

       Mamy wyznaczyć liczbę o 20 % mniejszą czyli 80 % tej liczby.

a)

              80 % × 15/8 = 0,8 × 15/8 = 3/2 = 1 i 1/2

             odp: liczba o 20 % mniejsza od   [tex]1\frac{7}{8}[/tex]  to  [tex]1\frac{1}{2}[/tex]

b)

                     80 % × 5/9 = 0,8 × 5/9 = 4/9

             odp: Liczba o 20 % mniejsza od 5/9 to 4/9

c)

                     80 % × 6/5 = 0,8 × 6/5 = 24/25

            odp: Liczba o 20% mniejsza od 6/5 to 24/25

d)

                    80 % × 55/64 = 0,8 × 55/64 = 11/16

            odp: Liczba o 20 % mniejsza od 55/64 to 11/16

zadanie 12

a) Długości boków tego trójkąta to: 4 cm, 4 cm oraz 3 cm.

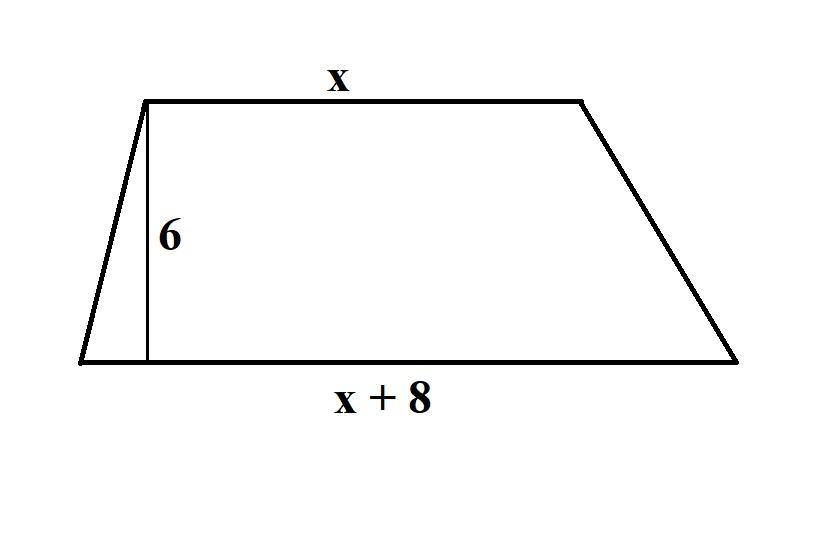
b) Krótsza podstawa trapezu ma długość 1 cm.

Rysunek pomocniczy w załączniku.

zadanie 13

Filiżanka bez podstawki kosztuje 23 złote.

Obliczanie długości boków trójkąta

Ramię trójkąta równoramiennego jest o 1 dłuższe od podstawy. Przyjmijmy za "x" długość podstawy, wtedy długość ramienia będzie miała x + 1 (zobacz rysunek). Wiemy, że obwód tego trójkąta to 11 cm. Obliczmy zatem "x" sumując każdy z boków trójkąta:

11 = x + x + 1 + x + 1

11 = 3x + 2

3x = 9

x = 3

Wiemy, że podstawa ma długość 3 cm, a zatem długość ramienia to 4 cm.

Obliczanie długości krótszej podstawy trapezu

Aby obliczyć jaką długość ma krótsza podstawa trapezu, oznaczmy ją jako "x", wtedy dłuższa podstawa będzie miała długość "x + 8" (zobacz rysunek). Wiemy, że pole tego trapezu to 30 cm². Wzór na pole trapezu jest następujący:

[tex]P=\frac{a+b}{2} *h[/tex]

gdzie:

a - długość krótszej podstawy,

b - długość dłuższej podstawy,

h - wysokość.

Podstawmy nasze dane do tego wzoru, pamiętając, że pole tego trapezu wynosi 30 cm²:

[tex]P=\frac{a+b}{2} *h\\30=\frac{x+x+8}{2}*6|*2\\ 60=6(2x+8)\\60=12x+48\\12x=12\\x=1[/tex]

Literką "x" oznaczyliśmy długość krótszej podstawy, a więc krótsza podstawa ma długość 1 cm.

W tym zadaniu przyjmijmy oznaczenia:

• x - cena podstawki
• x + 8 - cena filiżanki

Wiemy, że łącznie kosztują one 38 złotych. Zsumujmy więc te dwa wyrażenia:

x + x + 8 = 38

2x + 8 = 38

2x = 30

x = 15

Literką "x" oznaczyliśmy cenę podstawki. Cena filiżanki jest o 8 złotych droższa niż cena podstawki:

15 + 8 = 23 [zł]

Cena filiżanki bez podstawki wynosi 23 złote.

odpowiedź w załączniku myśle że pomogłam :)

odp w załączniku myślę że pomogłam :)