zadanie 2:
a) [tex]3^4-3^2=72[/tex]b) [tex]3^4*3^2 =3^6[/tex]c) [tex]3^4:3^2=3^2[/tex]d) [tex]3^4+3^2=90[/tex]e) [tex](2^{5})^{4} =2^{20}[/tex]f) [tex]4^0*3^2=1*3^2=3^2[/tex]
zadanie 3:
[tex]7^5*7^{11}=7^{16}=7^3*7^9*7^4\\7^8:7^4=7^4=(7^2)^2\\\frac{7^{35}}{7^{25}} =7^{10}=7^{30}:((7^4)^5)\\7^5*7^4=7^{9}=7^2*7^3*7^4\\7^{11}:7^{11}=7^0=7^{16}:7^{16}[/tex]
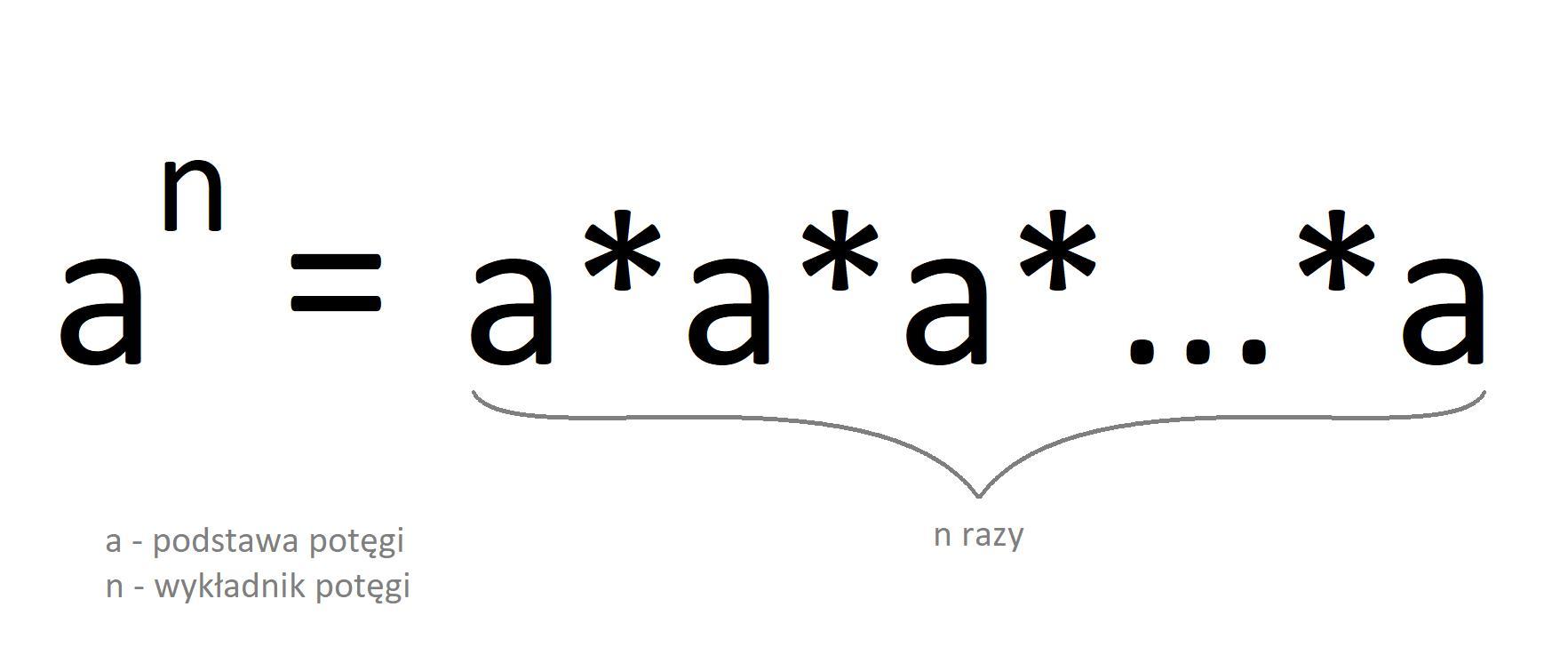
Potęgowanie to uproszczony sposób zapisu wielokrotnego mnożenia danego elementu przez siebie. Wykładnik potęgi informuje ile razy podstawa potęgi powinna być przez siebie wymnożona.
zadanie 2:
a) W tym przykładzie odejmujemy od siebie dwie potęgi o takiej samej podstawie i różnych wykładnikach. Aby policzyć takie wyrażenie wyciągamy przed nawias potęgę o niższym wykładniku. Obliczamy te wartości, mnożymy i zapisujemy wynik. [tex]3^4-3^2=3^2(3^2-1)= 9(9-1)=9*8=72[/tex]Nie ma możliwości skorzystania ze wzoru, obok wyrażenia wstawiamy znak -.
b) W tym przykładzie mnożymy przez siebie dwie potęgi o takiej samej podstawie i różnych wykładnikach. Przepisujemy zatem podstawę, a wykładniki dodajemy do siebie.[tex]3^4*3^2=3^{4+2} =3^6[/tex]Korzystamy ze wzoru: [tex]a^{m}* a^{n} =a^{m+n}[/tex], zapisujemy go obok wyrażenia.
c) W tym przykładzie dzielimy przez siebie dwie potęgi o takiej samej podstawie i różnych wykładnikach. Przepisujemy zatem podstawę, a wykładniki odejmujemy od siebie.[tex]3^4:3^2=3^{4-2} =3^2[/tex]Korzystamy ze wzoru: [tex]a^{m}:a^{n} =a^{m-n}[/tex], zapisujemy go obok wyrażenia.
d) W tym przykładzie dodajemy do siebie dwie potęgi o takiej samej podstawie i różnych wykładnikach. Aby policzyć takie wyrażenie wyciągamy przed nawias potęgę o niższym wykładniku. Obliczamy te wartości, mnożymy i zapisujemy wynik. [tex]3^4+3^2=3^2(3^2+1)= 9(9+1)=9*10=90[/tex]Nie ma możliwości skorzystania ze wzoru, obok wyrażenia wstawiamy znak -.
e) W tym przykładzie potęgujemy potęgę. Przepisujemy zatem podstawę, a wykładniki mnożymy przez siebie.[tex](2^{5})^{4} =2^{5*4} =2^{20}[/tex]Korzystamy ze wzoru: [tex](a^{m})^{n} =a^{m*n}[/tex], zapisujemy go obok wyrażenia.
f) W tym przykładzie mnożymy przez siebie potęgę o wykładniku równym zero oraz potęgę o innej podstawie i wykładniku.Każda liczba podniesiona do potęgi 0 jest równa 1, co można udowodnić na przykładzie:[tex]4^{-1}=\frac{1}{4}, 4^1=4, 4^2=16, 4^3=64[/tex] i tak dalej...Gdy wykładnik zwiększa się o 1 to wynik 4krotnie rośnie, a gdy wykładnik zmniejsza się o 1 to 4krotnie maleje, więc [tex]4^0=1[/tex].zatem: [tex]4^0*3^2=1*3^2=3^2[/tex]Nie korzystamy tu ze wzoru, obok wyrażenia wstawiamy znak -.Można też przekształcić to na postać: [tex]4^0*3^2=1*3^2=3^0*3^2=3^{0+2} =3^2[/tex], wówczas korzystamy ze wzoru: [tex]a^{m}* a^{n} =a^{m+n}[/tex], zapisujemy go obok wyrażenia.
zadanie 3:
Obliczamy działania z pierwszego i trzeciego wiersza, korzystając ze wzorów z tabelki w zadaniu drugim:
[tex]7^5*7^{11}=7^{16}\\7^8:7^4=7^{8-4}=7^4\\\frac{7^{35}}{7^{25}} = 7^{35}:7^{25}=7^{35-25}=7^{10}\\7^5*7^4=7^{5+4}=7^{9}\\7^{11}:7^{11}=7^{11-11}=7^0[/tex]
[tex]7^3*7^9*7^4=7^{3+9+4}=7^{16}\\7^{16}:7^{16}=7^0\\7^{30}:((7^4)^5)=7^{30}:7^{4*5}=7^{30}:7^{20}=7^{30-20}=7^{10}\\(7^2)^2=7^{2*2}=7^4\\7^2*7^3*7^4=7^{2+3+4}=7^9[/tex]
a zatem łączymy je tak, aby połączone były w następujące działania i potęgi:
[tex]7^5*7^{11}=7^{16}=7^3*7^9*7^4\\7^8:7^4=7^4=(7^2)^2\\\frac{7^{35}}{7^{25}} =7^{10}=7^{30}:((7^4)^5)\\7^5*7^4=7^{9}=7^2*7^3*7^4\\7^{11}:7^{11}=7^0=7^{16}:7^{16}[/tex]