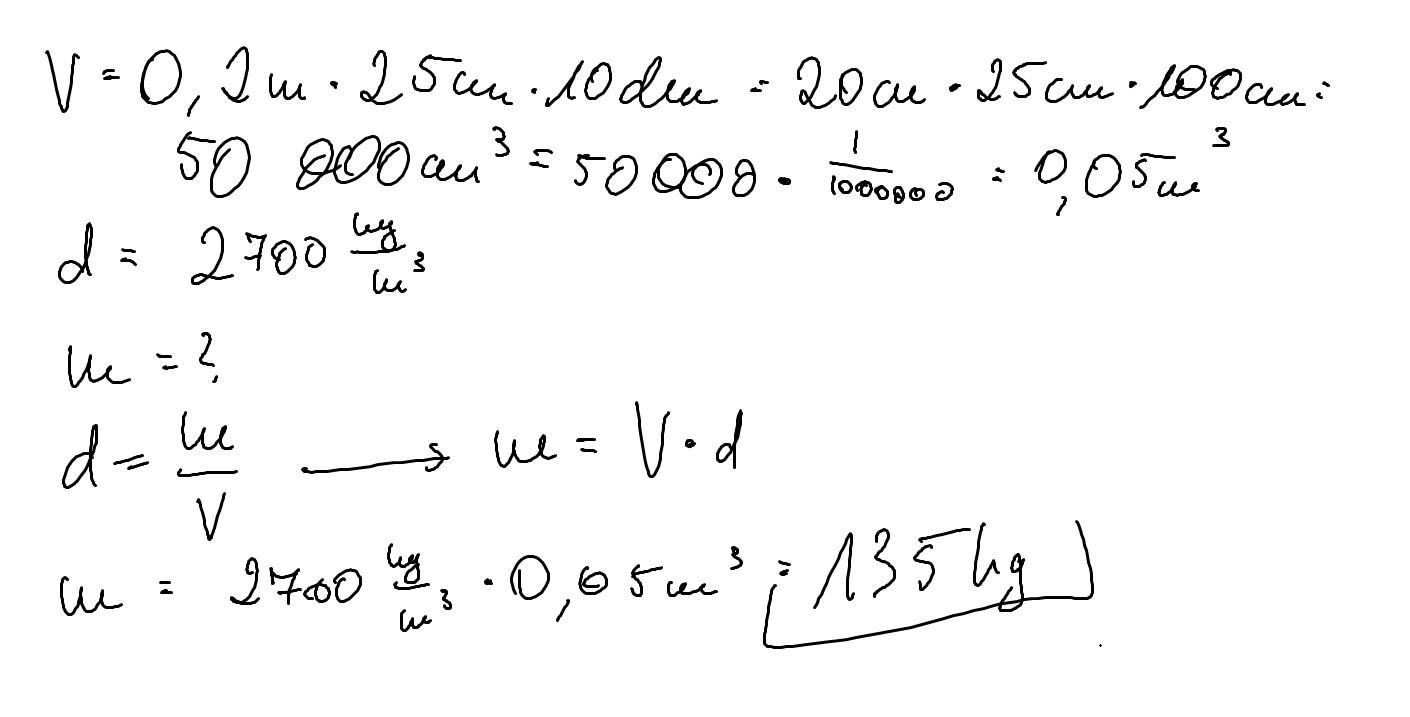Przedstaw hierarchię potrzeb człowieka zgodną z Twoich przekonaniami. Zacznij od potrzeb najistotniejszych i zakończ na tych najmniej ważniejszych. Oceń czy twoja propozycja spotkała by się z akceptacją większości osób z twojego otoczenia

Odpowiedzi 1

myślę że moja hierarchia wyglądałaby tak:potrzeby fizjologiczne (jedzenie, picie etc.),bezpieczeństwosamorealizacja (rozwój samego siebie i dążenie do celów)szacunekrozrywka (gry, książki, muzyka)moim zdaniem w tych czasach takie potrzeby bardzo pasują mi oraz obecnemu społeczeństwu i uważam, że większość osób mogłaby się zgodzić z moimi przekonaniami. pozdrawiam :)

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Zadanie rachunkowe. Jaką masę ma aluminiowy prostopadłościan o wymiarach: 0,2 m × 25 cm × 10 dm? Gęstość aluminium wynosi 2700 kg/m3. PLISSS SZYBKO!!!!!

Odpowiedź:

Wyjaśnienie:

V=abc

a=0,2 m   b=25 cm=0,25 m    c=10 dm=1 m

V=0,2*0,25*1=0,05 m^3

d=2700 kg/m^3

d=m/V /*V

m=dV

m=2700*0,05=135 kg

Odpowiedź:

Wyjaśnienie:

answer img
Oblicz długość krótszej przekątnej sześciokąta foremnego, którego dłuższa przekątna ma 7 cm.
question img

Odpowiedź:

Szukana krótsza przekątna ma długość  [tex]d = \frac{7\sqrt{3}}{2} \ cm.[/tex]

Szczegółowe wyjaśnienie:

Dłuższa przekątna sześciokąta foremnego D = 2a, gdzie a to długość boku sześciokąta.

Krótsza przekątna sześciokąta foremnego d = a√3.

Obliczamy długość boku sześciokąta:

[tex]D = 2a\\oraz\\D = 7 \ cm\\\\2a = 7 \ cm \ \ /:2\\\\a = \frac{7}{2} \ cm = 3,5 \ cm[/tex]

Obliczamy długość szukanej przekątnej:

[tex]d = \frac{7}{2}\cdot\sqrt{3} =\underline{\frac{7\sqrt{3}}{2} \ cm}[/tex]

Biologia klasa 72. Ułóż etapy procesu krzepnięcia krwi (A-E) w odpowiedniej kolejności. Zacznij od etapu oznaczonego literą B.A. Płytki krwi wydzielają substancję zmieniającą fibrynogen w fibrynę.B. Naczynie krwionośne ulega uszkodzeniu.C. Fibryna tworzy sieć, która zatrzymuje komórki krwi.D. Płytki krwi przyklejają się do brzegów rany.E. Sieć twardnieje, tworząc skrzep w ścianie naczynia.Z góry dziękuję za pomoc ​

Odpowiedź:

2 biologia

B. D. A. C. E

Liczę na naj

Proszę o pomoc w tym zadaniu dam mega sporo punktów zad 7 klasa 6 ćw
question img

Szczegółowe wyjaśnienie:

a) 2 500

b) 6 000

c) 11 000

d) 14 000

e) 200 000

f) 1 000

mam nadzieję że dobrze

Other WOS Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years