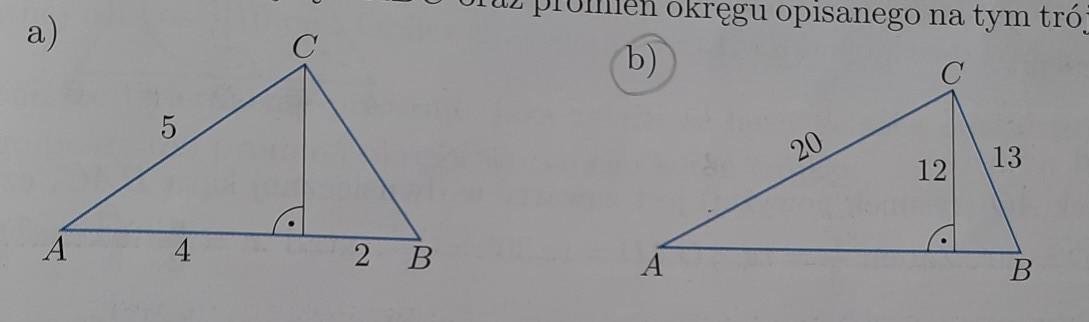Plisss Podaj siedem ryb o ciekawej budowieDaje Naj!Pliss
-
Temat:
Biologia -
Autor:
charliecraig -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
SZCZURZY OGON
ŻAGLICA
BELONA
PŁASZCZAK
BLOB FISH
MINÓG
WISŁONOS
ZĘBACZ SMUGOWY\
REKIN OLBRZYMI
REKIN GOBLIN
Wyjaśnienie:
LICZĘ NA NAJ <3
OSTRZEŻENIE ZANIM ZOBACZYCIE TE RYBY UŚWIADOMCIE SOBIE ŻE NIE CHECIE STRACIĆ OCZU XD
OBRZYDLIWE, STRASZNE
-
Autor:
pokeyeverett
-
Oceń odpowiedź:
4
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
jenny
-
Autor:
ascensióneu3j
-
Oceń odpowiedź:
0
-
Autor:
kennetholson
Odpowiedź:
[tex]a)~~P_{\Delta} =9~[j^{2}] ,~~R=\dfrac{5\sqrt{13} }{6} ~[j][/tex]
[tex]b)~~P_{\Delta} =126~[j^{2}] ,~~R=10\dfrac{5 }{6}~[j][/tex]
Szczegółowe wyjaśnienie:
Korzystamy ze wzorów:
- wzór na pole trójkąta [tex]P_{\Delta}=\dfrac{a\cdot h }{2} ~~gdzie ~~h-~~wysokosc~~poprowadzona~~do~~podstawy~~a.[/tex]
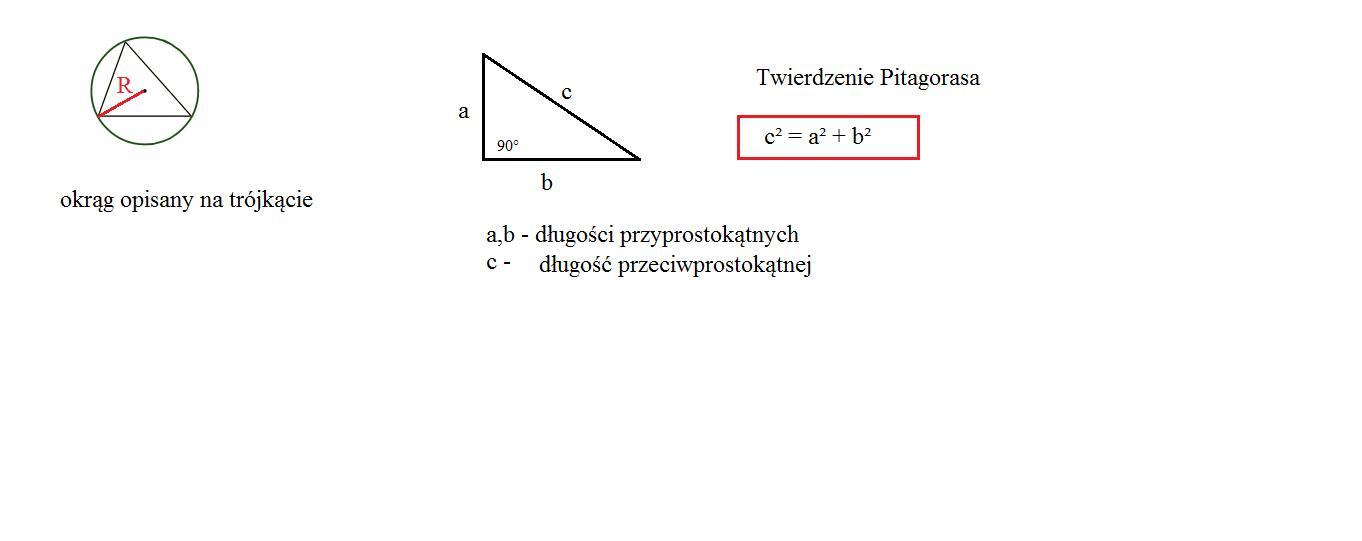
- stosujemy Twierdzenie Pitagorasa, które mówi, że kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych trójkąta prostokątnego (rysunek w załączniku)
- wzór na pole trójkąta [tex]P_{\Delta} =\dfrac{a\cdot b\cdot c}{4R}[/tex] , gdzie a,b,c - długości boków trójkąta, R- promień okręgu opisanego na trójkącie
- przekształcony wzór na pole trójkąta, by obliczyć promień okręgu opisanego na trójkącie [tex]R=\dfrac{a\cdot b \cdot c}{4P_{\Delta} }[/tex]
Rysunki pomocnicze w załączniku.
a)
Obliczamy długość boku I DC I =h oraz I BCI korzystając z Twierdzenia Pitagorasa.
[tex]\mid DC\mid =h\\\\(\mid AD\mid )^{2}+h^{2} =(\mid AC\mid )^{2}\\\\4^{2} +h^{2} =5^{2} \\\\h^{2} =25-16\\\\h^{2} =9~~\land~~h > 0~~\Rightarrow~~\boxed{h=3}[/tex]
[tex](\mid BC\mid )^{2}=h^{2} +(\mid DB\mid )^{2}\\\\(\mid BC\mid )^{2}=3^{2} +2^{2} \\\\(\mid BC\mid )^{2}=9+4\\\\(\mid BC\mid )^{2}=13~~\land~~\mid BC\mid > 0~~\Rightarrow~~\boxed{\mid BC\mid =\sqrt{13} }[/tex]
Obliczamy pole trójkąta.
[tex]P_{\Delta} =\dfrac{ \mid AB\mid \cdot h}{2} ~~\land~~\mid AB\mid=6~~\land~~h=3\\\\\boxed{P_{\Delta} =\dfrac{6\cdot 3}{2} =9~[j^{2}] }\\\\[/tex]
Obliczamy promień okręgu opisanego na tym trójkącie.
[tex]R=\dfrac{\mid AB \mid \cdot \mid BC \mid \cdot \mid AC \mid }{4\cdot P_{\Delta} } \\\\R=\dfrac{6\cdot \sqrt{13} \cdot 5 }{4\cdot 9 } \\\\\boxed{R=\dfrac{5\sqrt{13} }{6} ~[j]}[/tex]
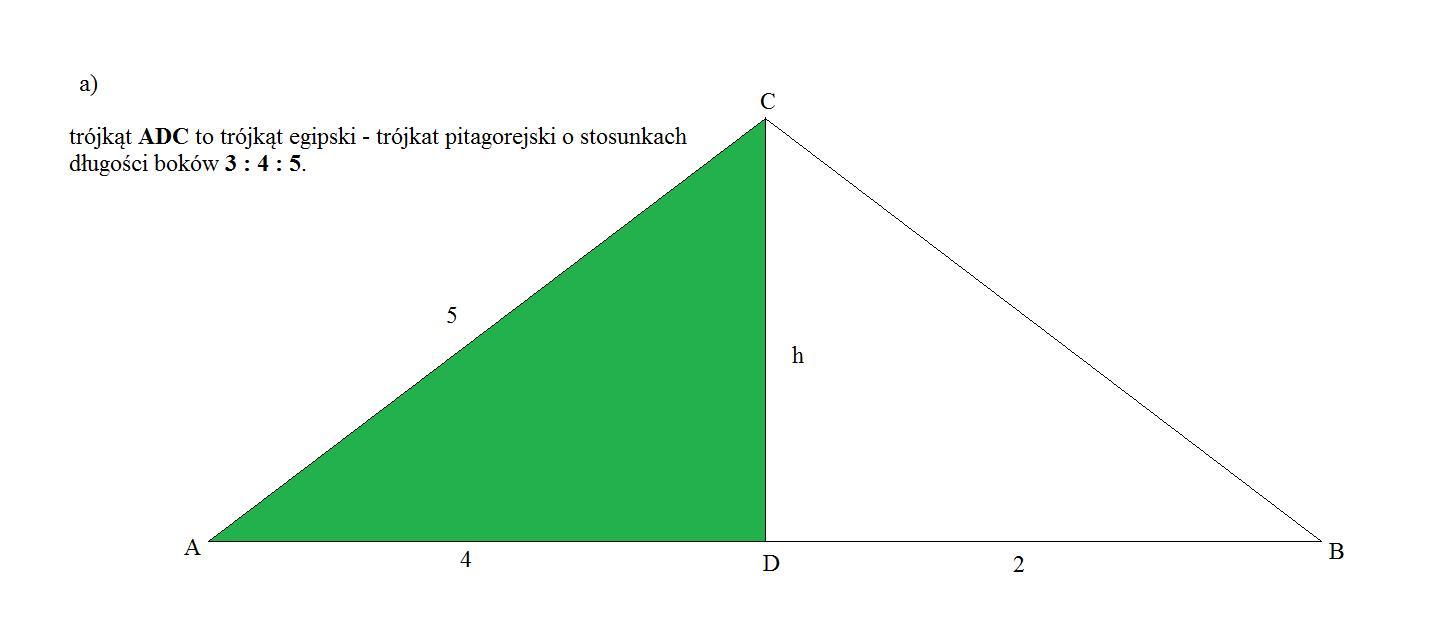
b)
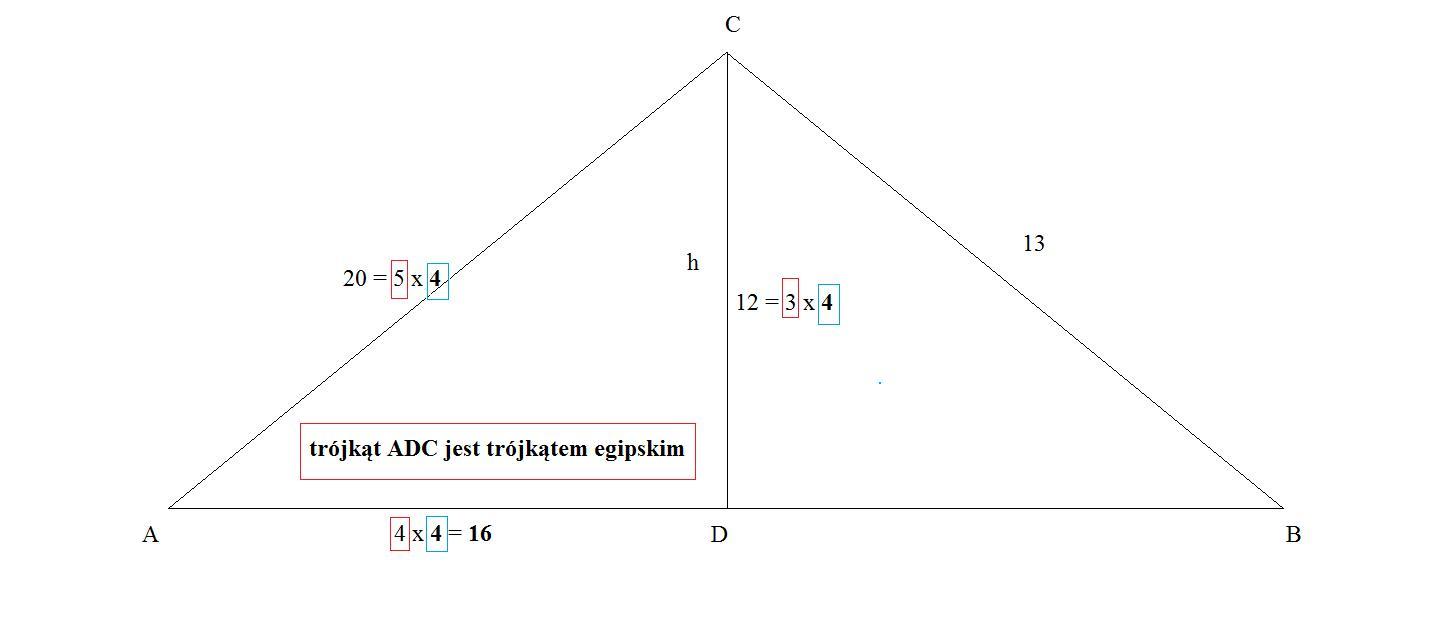
Obliczamy długość boku I DC I =h oraz I DCI korzystając z Twierdzenia Pitagorasa.
[tex]\mid DC\mid =h=\\\\(\mid AD\mid )^{2}+h^{2} =(\mid AC\mid )^{2}\\\\ (\mid AD\mid )^{2}+12^{2} =20^{2} \\\\ (\mid AD\mid )^{2} =400-144\\\\ (\mid AD\mid )^{2} =256~~\land~~ \mid AD\mid > 0~~\Rightarrow~~\boxed{ \mid AD\mid =3}[/tex]
[tex](\mid BC\mid )^{2}=h^{2} +(\mid DB\mid )^{2}\\\\(\mid DB\mid )^{2}=13^{2} -12^{2} \\\\(\mid DB\mid )^{2}=169-144\\\\(\mid DB\mid )^{2}=25~~\land~~\mid DB\mid > 0~~\Rightarrow~~\boxed{\mid DB\mid =5 }[/tex]
Obliczamy pole trójkąta.
[tex]P_{\Delta} =\dfrac{ \mid AB\mid \cdot h}{2} ~~\land~~\mid AB\mid=21~~\land~~h=12\\\\\boxed{P_{\Delta} =\dfrac{21\cdot 12}{2} =126~[j^{2}] }\\\\[/tex]
Obliczamy promień okręgu opisanego na tym trójkącie.
[tex]R=\dfrac{\mid AB \mid \cdot \mid BC \mid \cdot \mid AC \mid }{4\cdot P_{\Delta} } \\\\R=\dfrac{21\cdot 13 \cdot 20 }{4\cdot 126 }=\dfrac{1365}{126} =\dfrac{65}{6} \\\\\boxed{R=10\dfrac{5 }{6}~[j] }[/tex]
-
Autor:
ernesttlmy
-
Oceń odpowiedź:
9
-
Autor:
tannerholmes
-
Autor:
imogenpqxv
-
Oceń odpowiedź:
19