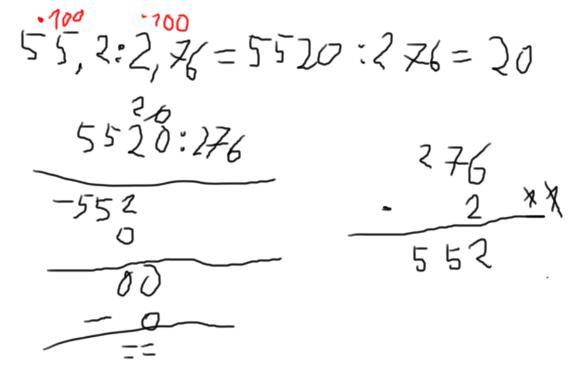proszę o pomoc ćwiczenia klasa 7 strona 109 zad oznaczone 4daje naj odrazu za dobrą odpowiedź ​

Odpowiedź:

Właściwy zbiór to C

Wyjaśnienie:

N to Niuton a ten to =kg * m/s2, kN to kiloniuton

Odpowiedź:

1

August II

-koronacja stanisława..

-wybuch wielkiej wojny

-podpisanie traktatu

-obrady sejmu

AugustIII

-Rywalizacja famili

-założenie Collegium

2 E, D, F, A, C, B

3

-zostaly zagwarantowane przez Katarzynę II

-prawa kordynalne

-rosyjscy dyplomaci mogli ingerować w sprawy wewnętrzne polski

4

literatyra piekna-df

literatura polityczna-egi

teatr-c

malarstwo-abh

5

panowanie króla stanisława Augusta Poniatowskiego, organizowanie obiadów czwartkowych, założenie szkoły rycerskiej, sprawowanie mecenatu

Wyjaśnienie:

Odpowiedź:

W przykładzie pierwszym obliczamy drogę z wzoru na pracę, czyli W=F·s. "s" jest tą naszą szukaną drogą, więc musimy przekształcić wzór.

Po lewej mamy pracę, a po prawej iloczyn drogi i siły. Szukamy siły, więc musimy zrobić tak, aby była ona sama na jednej stronie. Dlatego dzielimy całe wyrażenie przez siłę. Po prawej stronie praca się skróci i zostanie sama droga, a po lewej iloraz pracy i siły.

[tex]W=F\cdot s ~~/:F\\s=\frac{W}{F}[/tex]

Teraz wystarczy podstawić do wzoru w odpowiednich jednostkach. Praca w dżulach - J, a siła w niutonach - N. Wtedy droga wychodzi w jednostce układu Si, czyli w metrach - m.

W przykładzie drugim chcemy policzyć prędkość, gdy mamy daną moc. W podręczniku masz bardzo dobrze pokazane przekształcenie wzoru, więc to pominę. Po prostu do podstawowego wzoru na moc podstawiasz za prace wzór na nią, i wychodzi ci wzór prędkości pomnożony przez siłę. Ostatecznie otrzymujemy wzór P=F·v, z którego wyliczamy prędkość:

Dzielimy obie strony przez F. Po prawej stronie siła się skraca, a po lewej zostaje iloraz mocy i siły.

[tex]P=F\cdot v~~/:F\\v=\frac{P}{F}[/tex]

Teraz podstawiamy dane do wzoru również w odpowiednich jednostkach. Moc w watach - W, a siła w niutonach - N. prędkość wychodzi w jednostce podstawowej, czyli metrach na sekundę - [tex]\frac{m}{s}[/tex].

W podręczniku w drugim przykładzie podstawiono obje jednostki z przedrostkami kilo, które znaczą to, że podstawowa jednostka jest pomnożona przez tysiąc. W podstawowej jednostce te wartości wyglądałyby tak:

P=55,2kW=55200W

F=2,76kN=2760N

Po podstawieniu do wzoru można by było je skrócić przez tysiąc i wyszło by to samo.

20 to po prostu iloraz tych wartości.

55,2:2,76=20 - w załączniku podzielone pisemnie

Wyjaśnienie:

Odpowiedź:

c) komórka zwierzęca

Wyjaśnienie:

Wyjaśnienie:

Komórka roślinna liczę na naj