Do reakcji redukcji-utlenienia dobierz współczynniki stechiometryczne metodą bilansu elektronowego. PILNE!!!

• Największy wspólny dzielnik  NWD (a,b)  dwóch liczb całkowitych - to największa liczba naturalna, która  dzieli obie te liczby bez reszty.

• Najmniejsza wspólna wielokrotność  NWW(a,b) liczb naturalnych to najmniejsza liczba różna od zera, która jest jest jednocześnie wielokrotnością tych liczb.

Aby obliczyć NWD i NWW dwóch liczb naturalnych rozkładamy je na czynniki pierwsze, dzielimy każdą z liczb przez najmniejszą liczbę pierwszą , będącą jej dzielnikiem. Tak długo powtarzamy tę czynność , aż uzyskamy w wyniku liczbę 1.

• NWD (a,b) = iloczyn liczb występujących w obu rozkładach na czynniki pierwsze jednocześnie

• NWW(a,b) = iloczyn jednej liczby i czynników nie powtarzających się z rozkładu na czynniki pierwsze z drugiej liczby

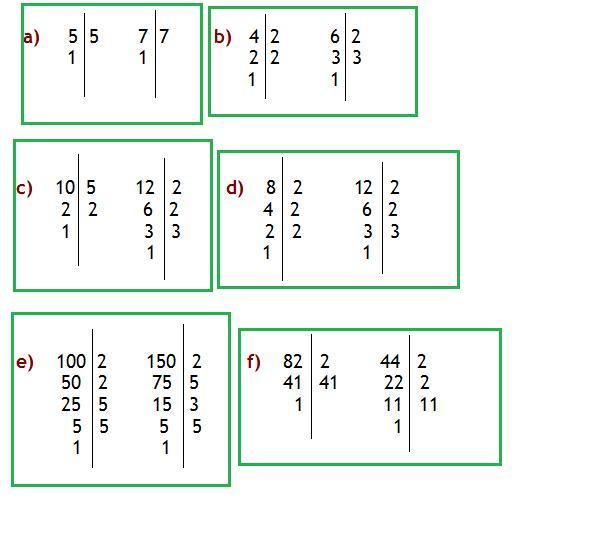
Rozkład par liczb na czynniki pierwsze w załączniku.

[tex]a)\\\\NWD(5,7)=1~~,~~NWW(5,7)=7\cdot 5 =35\\\\b)\\\\NWD(4,6)=2~~,~~NWW(4,6)=4\cdot 3 =12~~\lor~~NWW(4,6)=6\cdot 2 =12\\\\c)\\\\NWD(10,12)=2~~,~~NWW(10,12)=10\cdot 3\cdot 2 =60~~\lor~~NWW(10,12)=12\cdot 5 =60[/tex]

[tex]d)\\\\NWD(8,12)=2\cdot 2 = 4~~,~~NWW(8,12)=8\cdot 3 =24~~\lor~~NWW(8,12)=12\cdot 2 =24[/tex]

[tex]e)\\\\NWD(100,150)=2\cdot 5\cdot 5 =50~~,~~NWW(100,150)=100\cdot 3 =300~~\lor~~NWW(100,150)=150\cdot 2 =300[/tex]

[tex]f)\\\\NWD(82,44)=2~~,~~NWW(82,44)=82\cdot 2\cdot 11=1~804 ~~\lor~~NWW(82,44)=44\cdot 41 =1~804[/tex]

Sposoby komunikacji na odległość.

Komunikacje to forma porozumiewania się miedzy ludźmi.

Od najdawniejszych czasów formy komunikacji były różne:

• sygnalizacja ogniowa i dymna, miganie światełek przy pomocy luster,
• prymitywny" telegrafy puszczy" - tam tamy, bębny, rogi,
• pismo obrazkowe i literackie,
• poczta - już w w 2400 r. Egipcjanie dostarczali listy wykorzystując kurierów,

Po wynalezieniu elektryczności

• telegraf służył do przekazywania wiadomości tekstowych. Najbardziej znany to telegraf Morse oparty na systemie  kresek i kropek,

• radio (1896 r.), telewizja (1927 r), komputer ( (1897 r. )
• telefon odkryty przez A. Bella (1848 r. )
• telefon komórkowy ( 1073 r. )
• internet - przekaz satelitarny - pierwszego satelitę umieszczono na orbicie w 1962 r.  

Odpowiedź w załączniku:

Szczegółowe wyjaśnienie:

Odpoczynek poobiedni trwa 90 minut,a przygotowanie do obiadu trwa 15 minut, więc:

90 : 15 = 6

Odpoczynek poobiedni jest 6 razy dłuższy niż przygotowanie do obiadu.

Kwadrans to 15 min, więc

2* 15 min = 30 min

Taka różnica była między zajęciami artystycznymi ,a odpoczynkiem poobiednim

120 min - 90 min = 30 min

Między kreskami na diagramie zastosowana jest jednostką 10 min,ale można też podzielić oś co 5 min.

Odpowiedź:

młodszy syn- rozrzutny,lekko myślny, nieodpowiedzialny-cały majątek roztrwonił na zabawy i uczty

starszy syn-posłuszny, zazdrosny,pracowity,sprawiedliwy,dobry-był pracowity, zawsze słuchał ojca i służył mu pomocą, dlatego domagał się sprawiedliwości

ojciec- dobry,uczciwy,kochający-z radością przyjął syna który roztrwonił majątek i popełnił dużo błędów

Ps. myślę że pomogłam i życzę powodzenia w szkole