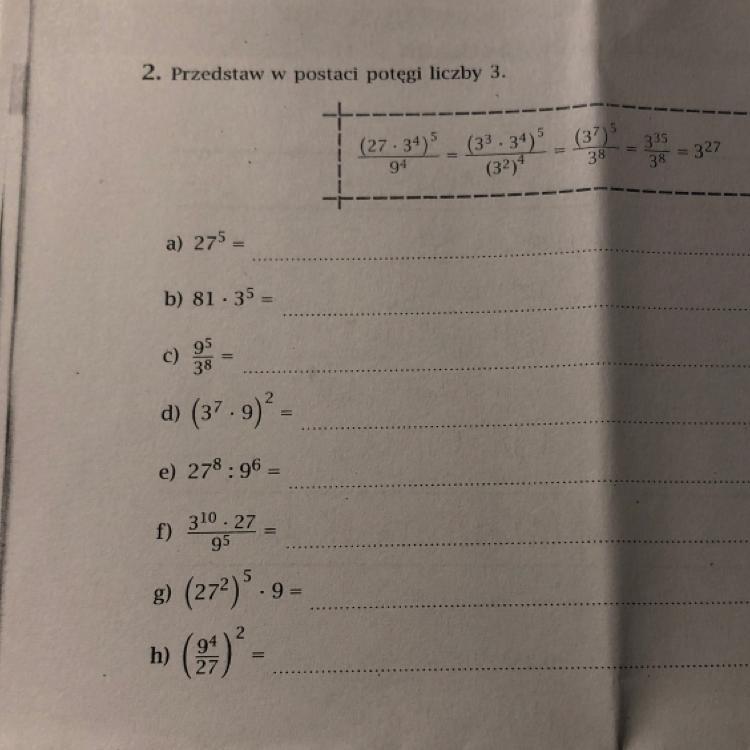Na sprężynie zawieszono ciężarek i wprawiono go w drgania o amplitudzie 2,4 mm oraz częstotliwości 0,9 hz. Jaka będzie częstotliwość drgań tego ciężarka, gdy amplituda drgań będzie równa 1,2 m? Uzasadnij odpowiedz.

Odpowiedź:

[tex]\huge\boxed{zad.2}[/tex]

[tex]\huge\boxed{a)~~27^{5}=3^{15}}[/tex]   [tex]\huge\boxed{b)~~81\cdot 3^{5}=3^{9}}[/tex]

[tex]\huge\boxed{c)~~\dfrac{9^{5}}{3^{8}} =3^{2}}[/tex]  [tex]\huge\boxed{d)~~(3^{7} \cdot 9)^{2}=3^{18}}[/tex]

[tex]\huge\boxed{e)~~27^{8}\div 9^{6}=3^{12}}[/tex]  [tex]\huge\boxed{f)~~\dfrac{3^{10}\cdot 27}{9^{5}} =3^{3}}[/tex]

[tex]\huge\boxed{g)~~(27^{2})^{5} \cdot 9= 3^{32}}[/tex]  [tex]\huge\boxed{h)~~\left( \dfrac{9^{4}}{27} \right)^{2}=3^{10}}[/tex]

Szczegółowe wyjaśnienie:

Korzystamy ze wzorów:

• [tex]x^{n} \cdot x^{m} =x^{n+m}[/tex]
• [tex]x^{n} \div x^{m}=\dfrac{x^{n}}{x^{m}} =x^{n-m},~~zal.~~x\neq 0[/tex]
• [tex](x^{n})^{m} =x^{n\cdot m }[/tex]
• [tex]x^{n} \cdot y^{n} =(x\cdot y)^{n}[/tex]
• [tex]x^{n} \div y^{n}=\dfrac{x^{n}}{y^{n}} =\left( \dfrac{x}{y} \right)^{n} ,~~zal.~~y\neq 0[/tex]

[tex]a)~~27^{5}=(3^{3})^{5}=3^{3\cdot 5} = \huge\boxed{3^{15}}[/tex]

[tex]b)~~81\cdot 3^{5}=3^{4}\cdot 3^{5}=3^{4+5}=\huge\boxed{3^{9} }[/tex]

[tex]c)~~\dfrac{9^{5}}{3^{8}} =\dfrac{(3^{2})^{5}}{3^{8}} =\dfrac{3^{2\cdot 5}}{3^{8}} =\dfrac{3^{10}}{3^{8}} =3^{10-8}=\huge\boxed{3^{2}}[/tex]

[tex]d)~~(3^{7} \cdot 9)^{2}=(3^{7} \cdot 3^{2})^{2}=(3^{7+2} )^{2}=(3^{9} )^{2}=3^{9\cdot 2}=\huge\boxed{3^{18}}[/tex]

[tex]e)~~27^{8}\div 9^{6}=(3^{3})^{8}\div (3^{2})^{6}=3^{3\cdot 8}\div 3^{2\cdot 6}=3^{24}\div 3^{12}=3^{24-12}=\huge\boxed{3^{12}}[/tex]

[tex]f)~~\dfrac{3^{10}\cdot 27}{9^{5}} =\dfrac{3^{10}\cdot 3^{3}}{(3^{2})^{5}} =\dfrac{3^{10+3}}{3^{2\cdot 5}} =\dfrac{3^{13}}{3^{10}} =3^{13-10}=\huge\boxed{3^{3}}[/tex]

[tex]g)~~(27^{2})^{5} \cdot 9=((3^{3})^{2})^{5} \cdot 3^{2}=3^{3\cdot 2\cdot 5 }\cdot 3^{2}=3^{30}\cdot 3^{2} =3^{30+2}=\huge\boxed{ 3^{32}}[/tex]

[tex]h)~~\left( \dfrac{9^{4}}{27} \right)^{2}=\left( \dfrac{(3^{2})^{4}}{3^{3}} \right)^{2}=\left( \dfrac{3^{2\cdot 4}}{3^{3}} \right)^{2}=\left( \dfrac{3^{8}}{3^{3}} \right)^{2}=(3^{8-3})^{2}=(3^{5})^{2}=3^{5\cdot 2} =\huge\boxed{3^{10}}[/tex]

Odpowiedź:

“kark"

wyniki:

-3cm

-2cm

-2,5cm

“ Górna część ręki"

wyniki:

-1,5cm

-2cm

-3,5cm

“Opuszek palca"

wyniki:

-0,5cm

-0,3cm

-0,7cm

Wniosek:

receptory dotyku są rozmieszczone nierównomiernie po całym ciele

Rzeczownik występujący w dopełniaczu liczby pojedynczej.

Końcówkę -ii piszemy w dopełniaczu, gdy wyraz jest obcego pochodzenia.

Końcówkę - i piszemy w dopełniaczu, gdy wyraz jest rodzimego pochodzenia.

Nie jestem pewien czy dobrze , ale tak mi się wydaje ;)